Kalkulus
Kalkulus (Bahasa Latin: calculus terbitan calx "batu kerikil; batu kecil; bara"[1] untuk menghitung[2]) adalah cabang ilmu matematik yang merangkumi had, terbitan, kamiran, dan deret tak terhingga. Kalkulus adalah ilmu mengenai perubahan, sebagaimana geometri adalah ilmu mengenai bentuk dan algebra adalah ilmu mengenai pengerjaan untuk memecahkan persamaan serta aplikasinya. Kalkulus mempunyai aplikasi yang luas dalam bidang-bidang sains, ekonomi, dan teknikal; serta dapat menyelesaikan pelbagai masalah yang tidak dapat diselesaikan dengan algebra asas.[3]
Kalkulus mempunyai dua cabang utama, iaitu kalkulus pembezaan dan kalkulus kamiran yang saling berhubungan melalui teorem asas kalkulus. Pelajaran kalkulus adalah pintu gerbang menuju pelajaran matematik lain yang lebih tinggi, yang khusus mempelajari fungsi dan limit, yang secara umum dinamakan analisis matematik.[3]
Sejarah[sunting | sunting sumber]
Sejarah perkembangan kalkulus dibahagikan kepada beberapa peringkat zaman iaitu zaman kuno, zaman pertengahan, dan zaman moden.
Zaman kuno[sunting | sunting sumber]
Pada zaman kuno, beberapa pemikiran tentang kalkulus integral telah muncul, tetapi tidak dikembangkan dengan baik dan teratur.[4] Pengiraan isipadu dan luas yang utama dalam kalkulus kamir ditelusuri kembali pada Papirus Moskwa zaman Mesir Purba s. 1800 SM yang menunjukkan kemampuan menghitung isipadu piramida terpancung.[5] Arkhimedes mengembangkan pemikiran ini lebih jauh dan menciptakan heuristik yang menyerupai kalkulus integral.[6]
Pada zaman pertengahan, Aryabhata di Patalipura (kini Patna di India) menggunakan konsep kecil ananta atau "tak terhingga" tahun 499 M dan menggambarkan masalah kiraan falak dalam bentuk persamaan membeza dasar.[7] Persamaan ini kemudian mendorong Bhāskara II pada abad ke-12 mengembangkan bentuk awal turunan yang mewakili perubahan yang sangat kecil takterhingga dan menjelaskan bentuk awal dari "Teorem Rolle".[8] Sekitar tahun 1000, Ibnu Haitham menjadi orang pertama yang merumuskan hitungan hasil jumlah pangkat empat, dan mengembangkan suatu kaedah permusuan umum dari hasil kuasa kamir integral yang sangat penting terhadap perkembangan kalkulus integral dengan menggunakan induksi , dia m.[9] Pada abad ke-12, Sharaf al-Din al-Tusi di Iran menemukan turunan dari fungsi kubik, sebuah hasil yang penting dalam kalkulus pembeza.[10] Pada abad ke-14, Madhava bersama ahli falak seperjuangannya di sekolah falak Kerala menjelaskan masalah khusus dari siri Taylor[11] yang dituliskan dalam teks Yuktibhasa.[12][13][14]
Zaman moden[sunting | sunting sumber]
Penemuan kiraan berkaitan bidang ini muncul sendiri di Jepun oleh Seki Kōwa pada awal abad ke-17. Di Eropah, beberapa matematikawan seperti John Wallis dan Isaac Barrow memberikan terobosan dalam kalkulus.[15] James Gregory membuktikan sebuah kasus khusus dari teorema dasar kalkulus pada tahun 1668.[16] Sir Isaac Newton dan Gottfried Wilhelm Leibniz telah menjalankan penyelidikan secara berasingan dan telah memberi sumbangan terbesar dalam kajian tersebut. Penyelidikan Sir Isaac Newton bermula apabila University of Cambridge ditutup pada tahun 1665 yang menyebabkan beliau terpaksa pulang ke tempat asalnya iaitu Lincolnshire.
Selama 18 bulan di sana, beliau telah mencipta ‘Method of Fluxions’, teori graviti dan teori cahaya. Berikutan dengan penciptaan teori-teori tersebut, beliau telah menulis sebuah buku yang berjudul ‘De Methodis Serierum et Fluxionum’ pada tahun 1671. Namun, Sir Isaac Newton telah gagal untuk menerbitkan buku tersebut. Buku tersebut tidak diterbitkan sehingga John Colson berjaya menerbitkannya dalam versi Bahasa Inggeris pada tahun 1736. Walau bagaimanapun, buku hasil tulisan Sir Isaac Newton tidak mempunyai simbol dan rumus.

Gottfried Wilhelm Leibniz telah memulakan penyelidikan beliau pada tahun 1673. Beliau merupakan tokoh yang telah mencipta simbol pembezaan dan pengamiran. Penerbitan pertamanya adalah pada tahun 1684 iaitu ‘Nova Methodus pro Maximis et Minimis, itemque Tangentibus’ dalam ‘Acta Eruditorum’, sebuah surat khabar yang diwujudkan pada tahun 1682 di Leipzig. Kemudian dua orang adik-beradik Bernoulli iaitu Jacob dan Johann mengambil idea tersebut dan mengembangkannya. Sejak kurun ke-17, penyelidikan tentang kalkulus telah mula berkembang dan mencapai tahap seperti yang sedia ada sekarang.
Prinsip[sunting | sunting sumber]
Had dan infinitesimal[sunting | sunting sumber]

Kalkulus pada umumnya dibangunkan dengan memanipulasi sejumlah kuantiti yang sangat kecil. Objek ini, yang boleh diperlakukan sebagai nombor, adalah sangat kecil. Sebuah bilangan dx yang infinitesimalnya dapat lebih besar daripada 0, namun lebih kecil daripada bilangan apapun tentang deret 1, ½, ⅓, ... dan bilangan nyata positif apapun. Setiap integer yang didarab dengan infinitesimal tetaplah infinitesimal, dengan kata lain kecil tak terhingga tidak memenuhi hotel Archimedes. Dari sudut pandang ini, kalkulus adalah sekumpulan teknik untuk memanipulasi infinitesimal.
Pada abad ke-19, konsep infinitesimal ini digantikan oleh konsep had. Had ini menjelaskan nilai suatu fungsi pada nilai input tertentu dengan keputusan daripada nilai input berdekatan. Dari sudut pandang ini, kalkulus adalah segugusan teknik memanipulasikan had-had tertentu.
Terbitan[sunting | sunting sumber]
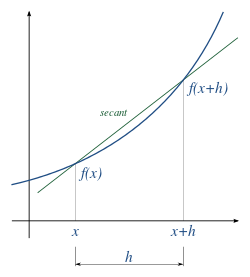
Terbitan dari suatu fungsi mewakili perubahan yang sangat kecil dari fungsi tersebut terhadap pembolehubahnya. Proses menemukan terbitan dari suatu fungsi disebut sebagai pembezaan.
Secara matematik, turunan fungsi ƒ(x) terhadap pemboleh ubah x adalah ƒ' yang nilainya pada titik x ialah:
- ,
dengan syarat wujudnya limit tersebut. Jika ƒ' eksis pada titik x tertentu, kita katakan bahawa ƒ dibezakan (mempunyai keturunan) pada x, dan jika ƒ' eksis di setiap titik pada domain ƒ, kita sebut ƒ terdiferensialkan.
Rujukan[sunting | sunting sumber]
- ^ "calcŭlus". K. Prent, J. Adisubrata, W. J. S. Poerwadarminta (1969). Kamus Latin-Indonesia. Jogjakarta: Penerbitan Jajasan Kanisius. m/s. 106.
- ^ Lihat:
- "History – Were metered taxis busy roaming Imperial Rome?". Skeptics Stack Exchange. 2020-06-17. Diarkibkan daripada yang asal pada 25 May 2012. Dicapai pada 2022-02-13.
- Cousineau, Phil (2010). Wordcatcher: An Odyssey into the World of Weird and Wonderful Words (dalam bahasa Inggeris). Simon and Schuster. m/s. 58. ISBN 978-1-57344-550-4. OCLC 811492876.
- ^ a b Latorre, Donald R.; Kenelly, John W.; Reed, Iris B.; Biggers, Sherry (2007), Calculus Concepts: An Applied Approach to the Mathematics of Change, Cengage Learning, m/s. 2, ISBN 0-618-78981-2, diarkibkan daripada yang asal pada 2023-03-27, dicapai pada 2013-11-08 Unknown parameter
|dead-url=ignored (bantuan), Chapter 1, p 2 Diarkibkan 2023-03-27 di Wayback Machine - ^ Morris Kline, Mathematical thought from ancient to modern times, Vol. I
- ^ Helmer Aslaksen. Why Calculus? Diarkibkan 2010-10-14 di Wayback Machine National University of Singapore.
- ^ Archimedes, Method, in The Works of Archimedes ISBN 978-0-521-66160-7
- ^ "Aryabhata the Elder". Diarkibkan daripada yang asal pada 2015-07-11. Dicapai pada 2007-08-09. Unknown parameter
|dead-url=ignored (bantuan) - ^ Ian G. Pearce. Bhaskaracharya II. Diarkibkan 2016-09-01 di Wayback Machine
- ^ Victor J. Katz (1995). "Ideas of Calculus in Islam and India", Mathematics Magazine 68 (3), hlm. 163-174.
- ^ J. L. Berggren (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", Journal of the American Oriental Society 110 (2), hlm. 304-309.
- ^ "Madhava". Biography of Madhava. School of Mathematics and Statistics University of St Andrews, Scotland. Diarkibkan daripada yang asal pada 2006-05-14. Dicapai pada 2006-09-13. Unknown parameter
|dead-url=ignored (bantuan) - ^ "An overview of Indian mathematics". Indian Maths. School of Mathematics and Statistics University of St Andrews, Scotland. Diarkibkan daripada yang asal pada 2006-07-03. Dicapai pada 2006-07-07. Unknown parameter
|dead-url=ignored (bantuan) - ^ "Science and technology in free India" (PDF). Government of Kerala — Kerala Call, September 2004. Prof.C.G.Ramachandran Nair. Diarkibkan daripada yang asal (PDF) pada 2006-08-21. Dicapai pada 2006-07-09. Unknown parameter
|dead-url=ignored (bantuan) - ^ Charles Whish (1835). Transactions of the Royal Asiatic Society of Great Britain and Ireland.
- ^ The geometrical lectures of Isaac Barrow, translated, with notes and proofs, and a discussion on the advance made therein on the work of his predecessors in the infinitesimal calculus. Chicago: Open Court. 1916.
- ^ Ralat petik: Tag
<ref>tidak sah; teks bagi rujukanSimmonstidak disediakan


