Logaritma biasa
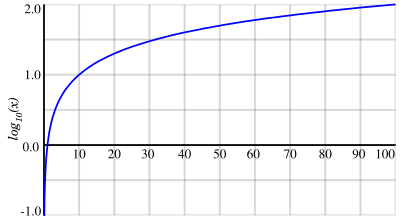
Dalam bidang matematik, logaritma biasa bermaksud logaritma asas 10. Ia juga dikenali sebagai logaritma dekadik dan juga logaritma perpuluhan, dinamakan sempena nombor asasnya, ataupun logaritma Briggsian, sempena Henry Briggs, seorang ahli matematik Inggeris yang menjadi perintis penggunaannya. Ia ditandakan dengan log10(x), atau kadang-kadang Log(x) dengan huruf L besar (namun demikian, notasi sebegini kabur memandangkan ia boleh bermaksud fungsi berbilang nilai logaritma asli kompleks). Pada mesin kira, ia selalunya dilabelkan sebagai "log", tetapi ahli matematik selalunya merujuk kepada logaritma asli dan bukannya logaritma biasa apabila mereka menulis "log". Untuk mengelakkan kekaburan, spesifikasi ISO menyatakan bahawa log10(x) seharusnya ditulis sebagai lg (x) manakala loge(x) ditulis sebagai ln (x).
Penggunaan[sunting | sunting sumber]
Sebelum awal 1970an, kalkulator elektronik masih belum meluas penggunaannya. Berikutan dengan keupayaannya untuk menyimpan kerja dalam pendaraban dan pembahagian dengan kertas dan pen, buku sifir logaritma asas 10 disediakan di ruangan lampiran kebanyakan buku. Sifir "logaritma biasa" sebegitu menyatakan nilai logaritma, biasanya sehingga 4 hingga 5 tempat perpuluhan, bagi setiap nombor di lajur sebelah kanan, yang merangkumi nombor dari 1 hingga 10 dengan pecahan lebih kecil, barang kali 0.01 atau 0.001. Hanya nilai dari 1 hingga 10 sahaja diperlukan, memandangkan logaritma nombor-nombor lebih besar boleh dikira dengan mudah.
Contohnya, logaritma bagi 120 diberi sebagai:
Nombor terakhir (0.079181) — bahagian pecahan bagi logaritma bagi 120, dikenali sebagai mantisa bagi logaritma biasa bagi 120 — boleh didapati di dalam sifir.[note 1] Lokasi titik perpuluhan bagi 120 menyatakan bahagian integer bagi logaritma biasa 120, dipanggil perwatakan bagi logaritma biasa 120, iaitu 2.
Nombor antara (dan tidak termasuk) 0 dan 1 mempunyai logaritma negatif. Contohnya,
Untuk mengelakkan keperluan sifir berasingan bagi menukarkan logaritma positif dan negatif kembali kepada nombor-nombor asalnya, notasi bar digunakan:
Bar di atas perwatakan menandakan bahawa ia adalah negatif sedangkan mantisa kekal positif.
| nombor | logaritma | perwatakan | mantisa | bentuk gabungan |
|---|---|---|---|---|
| n (= 5 × 10i) | log10(n) | i (= lantai(log10(n)) ) | log10(n) − perwatakan | |
| 5 000 000 | 6.698 970... | 6 | 0.698 970... | 6.698 970... |
| 50 | 1.698 970... | 1 | 0.698 970... | 1.698 970... |
| 5 | 0.698 970... | 0 | 0.698 970... | 0.698 970... |
| 0.5 | −0.301 029... | −1 | 0.698 970... | 1.698 970... |
| 0.000 005 | −5.301 029... | −6 | 0.698 970... | 6.698 970... |
Sila ambil perhatian bahawa mantisa adalah lazim bagi kesemua nilai 5×10i. Buku sifir logaritma mempunyai hanya satu entri diindekskan bagi mantisa yang sama. Dalam contoh, 0.698 970 (004 336 018 ...) akan disenaraikan sekali diindekskan dengan 5, atau mungkin dengan 0.5 atau 500 dsb..
Contoh berikut menggunakan notasi bar bagi mengira 0.012 × 0.85 = 0.0102:
* Langkah ini menjadikan mantisa terletak antara 0 hingga 1, supaya antilognya (10mantissa) boleh dicari dengan mudah.

Sejarah[sunting | sunting sumber]
Logaritma biasa kadang kala dipanggil sebagai "logaritma Briggsian" sempena Henry Briggs, seorang ahli matematik British abad ke-17.
Disebabkan logaritma asas 10 paling berguna dalam membuat pengiraan, jurutera secara amnya menulis "log(x)" apabila mereka bermaksud log10(x). Ahli matematik sebaliknya menulis "log(x)" apabila mereka bermaksud loge(x) untuk logaritma asli. Hari ini, kedua-dua notasi sebegini ditemui. Memandangkan kalkulator elektronik tangan direka oleh jurutera dan bukannya ahli matematik, maka sudah menjadi adat untuk mengikut notasi jurutera. Maka dari segi notasi, menurut kepada yang mana menulis "ln(x)" apabila bermaksud logaritma asli, mungkin telah dipopularkan oleh satu ciptaan yang menjadikan istilah "logaritma biasa" kurang lazim, iaitu kalkulator elektronik.
Nilai nombor[sunting | sunting sumber]
Nilai nombor bagi logaritma asas 10 boleh dikira menggunakan identiti berikut.
sebagai prosedur yang wujud bagi menentukan nilai nombor logaritma asas e dan logaritma asas 2.
Lihat juga[sunting | sunting sumber]
Nota[sunting | sunting sumber]
- ^ Ia berakar umbi daripada makna lama bukan nombor bagi perkataan mantissa: tambahan kecil, misalnya bagi satu teks. Bagi maksud lebih moden bagi perkataan mantissa, rujuk signifikand.
Rujukan[sunting | sunting sumber]
- Michael Möser: Engineering Acoustics: An Introduction to Noise Control. Springer 2009, ISBN 978-3-540-92722-8, p. 448 ([ restricted online copy], m/s. 448, di Buku Google)
- A. D. Poliyanin, A. V. Manzhirov: Handbook of mathematics for engineers and scientists. CRC Press 2007, ISBN 978-1-58488-502-3, p. 9 ([ restricted online copy], m/s. 9, di Buku Google)
Pautan luar[sunting | sunting sumber]
- Logaritma Briggsian, PlanetMath.org. termasuklah contoh terperinci mengenai cara menggunakan sifir logaritma





