Titik Lagrange


Klik untuk animasi.
Titik Lagrange (titik L atau titik librasi) adalah lima kedudukan di dalam sebuah konfigurasi orbit yang mana sesebuah objek kecil yang dipengaruhi oleh graviti sahaja boleh secara teori menjadi sebahagian daripada suatu corak bentuk malar dengan dua objek lebih besar (seperti satelit yang berkenaan dengan Bumi dan Bulan). Titik-titik Lagrange menandai kedudukan di mana gabungan tarikan graviti dua jasad besar membekalkan daya memusat setepatnya yang diperlukan untuk orbit bersama mereka.
Titik Lagrange merupakan penyelesaian pola malar kepada masalah tiga jasad yang terbatas. Contohnya, dengan dua buah jasad besar dalam orbit-orbit yang mengelilingi satu pusat jisim yang dikongsi oleh dua jasad itu, terdapat lima kedudukan di angkasa di mana boleh terletaknya sesebuah jasad ketiga yang tidak begitu ketara jisimnya untuk mengekalkan kedudukannya secara nisbi dengan dua jasad besar. Seperti yang dilihat dalam rangka rujukan berpusat yang sepadan dengan halaju sudut kedua-dua jasad seorbit itu, medan graviti dua jasad besar itu adalah seimbang dengan pecutan satelit di titik-titik Lagrange, membolehkan jasad ketiga itu untuk kekal pegun secara nisbi dengan dua jasad terdahulu.[2]
Sejarah dan konsep[sunting | sunting sumber]
Tiga titik Lagrange kolinear (L1, L2, L3) sudah ditemui oleh Leonhard Euler beberapa tahun sebelum Lagrange menemui yang dua lagi.[3][4]
Pada tahun 1772, Joseph Louis Lagrange menerbitkan "Esei mengenai masalah tiga jasad". Dalam bab pertama, beliau membincangkan masalah tiga jasad yang umum. Daripada itu, dalam bab kedua, beliau mendemonstrasikan dua penyelesaian pola malar istimewa, iaitu yang kolinear dan yang sama sisi, untuk mana-mana tiga jasad yang berorbit bulat.[5]
Titik-titik Lagrange[sunting | sunting sumber]
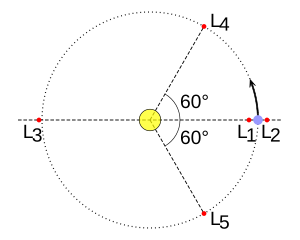

Lima titik Lagrange dilabelkan dan ditakrifkan seperti berikut:
L1[sunting | sunting sumber]
Titik L1 terletak pada garis yang ditakrifkan oleh dua jasad besar M1 dan M2, dan di antara kedua-dua jasad tersebut. Ianya titik Lagrange yang paling difahami secara intuisi, iaitu satu yang mana tarikan graviti M2 menutup separa tarikan graviti M1.
- Contoh: Sesebuah objek yang mengorbit Matahari dengan lebih dekat daripada Bumi biasanya lebih singkat tempoh orbitnya berbanding Bumi, tetapi itu tidak mengambil kira kesan tarikan graviti Bumi sendiri. Jika objek itu langsung berada di antara Bumi dan Matahari, maka graviti Bumi melemahkan daya yang menarik objek tersebut ke arah Matahari, dan oleh itu melanjutkan tempoh orbit objek tersebut. Makin dekat objek itu dengan Bumi, makin besar kesannya. Di titik L1, tempoh orbit objek itu menjadi bersamaan tepat dengan tempoh orbit Bumi. L1 terletak kira-kira 1.5 juta kilometer dari Bumi.[6]
Lokasi L1 adalah penyelesaian kepada persamaan berikut yang mengimbangi gravitasi dan daya memusat:
yang mana r adalah jarak titik L1 dari objek yang lebih kecil, R adalah jarak di antara dua objek utama, M1 dan M2 adalah jisim masing-masing bagi objek besar dan kecil. (Kuantiti dalam tanda kurungan kanan ialah jarak L1 dari pusat jisim.) Penyelesaian persamaan ini untuk r melibatkan penyelesaian kuintik, tetapi jika jisim M2 jauh lebih kecil daripada M1 maka L1 dan L2 adalah lebih kurang bersamaan dengan r, iaitu bersamaan dengan jejari sfera Hill, iaitu:
Jarak ini boleh diterangkan sebagai sebegitu mana tempoh orbit yang bersamaan dengan orbit bulat dengan jarak ini sebagai jejari di keliling M2 jika tiadanya M1, adalah bersamaan dengan jejari M2 di keliling M1 dibahagi dengan :
L1 Matahari–Bumi sesuai untuk melakukan pencerapan terhadap sistem Matahari–Bumi, di mana objek-objeknya tidak sesekali dibayangi oleh Bumi atau Bulan. Misi pertama yang sedemikian adalah misi International Sun Earth Explorer 3 (ISEE3) yang digunakan sebagai pemantau ribut amaran awal antara planet untuk gangguan suria. Kebolehlaksanaan orbitnya adalah hasil daripada tesis PhD oleh ahli astrodinamik, Robert W. Farquhar.[7] Kemudiannya, Solar and Heliospheric Observatory (SOHO) ditempatkan di suatu orbit Halo pada L1, dan Advanced Composition Explorer (ACE) di suatu orbit Lissajous, juga pada titik L1. WIND juga terletak di L1.
L1 Bumi–Bulan membolehkan capaian yang agak mudah kepada orbit-orbit Bulan dan Bumi tanpa perubahan ketara pada halaju, dan oleh itu mendapat kelebihan untuk mendudukkan stesen angkasa bermanusia separuh jalan yang bertujuan untuk memudahkan pengangkutan kargo dan kakitangan berulang-alik ke Bulan.
Dalam sistem bintang perduaan, lobus Roche terletak puncaknya di L1; sebarang bintang yang melimpahi lobus Rochenya akan kehilangan jirim kepada bintang temannya.

Titik L1 juga penting untuk satelit penyelidikan sains.
L2[sunting | sunting sumber]

Titik L2 terletak pada garis yang melalui dua jasad besar, hanya di luar jasad mana yang lebih kecil. Di sini, daya graviti kedua-dua jasad besar itu mengimbangi kesan memusat terhadap sesebuah jasad pada L2.
- Contoh: Di muka Bumi yang menoleh dari Matahari, tempoh orbit sesebuah objek biasanya lebih lanjut daripada tempoh orbit Bumi. Tarikan tambahan dari graviti Bumi mengurangkan tempoh orbit objek tersebut, dan pada titik L2-lah objek itu menjadi bersamaan tempoh orbitnya dengan Bumi.
Titik L2 Matahari–Bumi adalah tempat yang sesuai untuk balai cerap asas angkasa. Oleh sebab sesebuah objek di sekitar L2 akan mengekalkan kedudukan nisbi yang sama berkenaan dengan Matahari dan Bumi, maka pemerisaian dan penentukurannya jauh lebih mudah. Bagaimanapun, ianya sedikit di luar capaian umbra Bumi,[8] maka sinaran Matahari tidak dihalang sepenuhnya. Balai cerap angkasa Planck sudah pun di dalam orbit di sekitar L2 Matahari–Bumi, begitu juga dengan Herschel (hingga Jun 2013[9]), Chang'e 2 (hingga April 2012[10][11]) dan Kuar Anistropi Gelombang Mikro Wilkinson[12] (hingga Oktober 2010). Kuar Gaia dan Teleskop Angkasa Lepas James Webb bakal ditempatkan di L2 Matahari–Bumi.
Titik L2 Bumi–Bulan mungkin lokasi yang sesuai untuk satelit komunikasi yang meliputi muka jauh Bulan, dan juga suatu "lokasi idaman" untuk depot bahan dorong dalam cadangan seni bina pengangkutan angkasa berasaskan depot.[13]
Lokasi L2 adalah penyelesaian kepada persamaan berikut yang mengimbangi gravitasi dengan daya memusat:
dengan parameter-parameter yang sama takrifannya dengan perihal L1. Sekali lagi, jika jisim M2 jauh lebih kecil daripada jisim M1, maka L2 adalah lebih kurang sama dengan jejari sfera Hill, iaitu:
Contoh[sunting | sunting sumber]
- Matahari dan Bumi: 1,500,000 km (930,000 bt) dari Bumi
- Bumi dan Bulan: 60,000 km (37,000 bt) dari Bulan[14]
L3[sunting | sunting sumber]
Titik L3 terletak pada garis yang ditentukan oleh kedua-dua jasad besar, hanya di luar jasad mana yang lebih besar.
- Contoh: L3 dalam sistem Matahari–Bumi wujud di muka bertentangan Matahari, sedikit di luar orbit Bumi tetapi sedikit lebih dekat daripada Matahari berbanding Bumi. ('Pertindanan' ini adalah kerana Matahari juga dipengaruhi oleh graviti Bumi, dan oleh itu mengorbit di keliling baripusat kedua-dua jasad yang sebenarnya di dalam Matahari.) Di titik L3, gabungan tarikan Bumi dengan Matahari sekali lagi menyebabkan objek berkenaan untuk mengorbit sama lama dengan Bumi.
Lokasi L3 adalah penyelesaian kepada persamaan berikut yang mengimbangi gravitasi dan daya memusat:
dengan parameter-parameter yang ditakrifkan seperti mana dalam perihak L1 dan L2, kecuali r kini menandakan berapa dekatnya L3 kepada objek yang lebih besar daripada objek yang lebih kecil. Jika jisim M2 kurang daripada M1 maka:
Sesebuah kuar angkasa yang mengorbit berhampiran titik L3 Matahari–Bumi tentu dapat mencerap dengan dekat evolusi kawasan tompok matahari yang aktif sebelum berputar ke dalam kedudukan geoefektif, supaya amaran seawal 7 hari boleh dikeluarkan oleh Pusat Peramalan Cuaca Angkasa Lepas NOAA. Lebih-lebih lagi, sesebuah satelit berdekatan titik L3 Matahari–Bumi akan membekalkan pemerhatian yang amat penting bukan sahaja untuk ramalan Bumi, bahkan juga untuk bantuan di angkasa lepas (ramalan Marikh dan untuk misi bermanusia ke asteroid dekat Bumi). Pada tahun 2010, telah dikajinya trajektori pemindahan kuar angkasa ke L3 Matahari–Bumi dan sesetengah reka-ciptaan telah dipertimbangkan.[15]
Salah satu contoh asteroid yang melintasi titik L3 adalah rumpun Hilda yang dibawa oleh orbitnya ke titik L3 Matahari–Musytari.
L4 dan L5[sunting | sunting sumber]

Titik-titik L4 dan L5 terletak di sudut ketiga bagi dua segi tiga sama sisi di satah orbit yang tapak sepunyanya adalah garis di antara kedua-dua pusat jasad tersebut, yang mana titik itu berada di belakang (L5) atau di hadapan (L4) jasad yang lebih kecil berkenaan dengan orbitnya di keliling jasad yang lebih besar.
Titik-titik ini seimbang kerana di L4 dan L5, jarak dengan kedua-dua jasad adalah setara. Sehubungan itu, daya graviti dari kedua-dua jasad besar itu berada pada nisbah yang sama dengan jisim kedua-dua jasad, dan oleh itu daya paduan bertindak melalui baripusat sistem; selain itu, geometri segi tiga itu memastikan bahawa pecutan paduan adalah ke arah dari baripusat pada nisbah yang sama dengan dua jasad besar itu. Dengan baripusat sebagai pusat jisim dan pusat putaran sistem sekali gus, daya paduan ini bertepatan dengan yang diperlukan untuk mengekalkan sesebuah jasad pada titik Lagrange dalam keseimbangan orbit dengan seluruh sistem. (Sesungguhnya jasad ketiga tidak memerlukan jisim yang tidak ketara). Konfigurasi segi tiga umum ditemui oleh Lagrange sewaktu mengerjakan masalah tiga jasad.
L4 dan L5 adakalanya bergelar titik Lagrange segi tiga atau titik trojan. Nama titik Trojan adalah bersempena asteroid-asteroid Trojan pada titik-titik L4 dan L5 Matahari–Musytari. Asteroid-asteroid pada titik L4 yang mendepani Musytari dipanggil "kem Yunani", while those at the L5 point are referred to as the "kem Trojan". Asteroid ini rata-rata dinamai sempena tokoh-tokoh dari kem masing-masing dalam Perang Troy.
Contoh[sunting | sunting sumber]
- Titik-titik L4 dan L5 Matahari–Bumi masing-masing terletak 60° di hadapan dan 60° di belakang Bumi yang mengorbit Matahari. Kawasan-kawasan di sekitar titik-titik ini mengandungi debu antara planet dan sekurang-kurangnya sebuah asteroid, 2010 TK7, yang dikesan pada Oktober 2010 oleh WISE dan diumumkan pada Julai 2011.[16][17]
- Titik-titik L4 dan L5 Bumi–Bulan masing-masing terletak 60° di hadapan dan 60° di belakang Bulan yang mengorbit Bumi. Ia mungkin mengandungi debu antara planet di dalam apa yang dipanggil awan Kordylewski; bagaimanapun, Pengira Debu Munich (MDC) pada kuar angkasa Hiten tidak mengesan sebarang peningkatan pada debu apabila ia melintasi kedua-dua titik ini.
- Kawasan di sekitar titik-titik L4 dan L5 Matahari–Musytari diduduki oleh asteroid Trojan.
- Kawasan di sekitar titik-titik L4 dan L5 Matahari–Neptun mempunyai objek-objek trojan.[18]
- Tethys iaitu bulan Zuhal mempunyai dua satelit yang lebih kecil pada titik-titik L4 dan L5nya iaitu masing-masing Telesto dan Calypso.
- Dione iaitu bulan Zuhal mempunyai dua satelit yang lebih kecil pada titik-titik L4 dan L5nya iaitu masing-masing Helene dan Polydeuces.
Catatan[sunting | sunting sumber]
Rujukan[sunting | sunting sumber]
- ^ ZF Seidov, "The Roche Problem: Some Analytics", The Astrophysical Journal, 603:283-284, 2004 March 1
- ^ "Lagrange Points" oleh Enrique Zeleny, Wolfram Demonstrations Project.
- ^ Koon, W. S. (2006). Dynamical Systems, the Three-Body Problem, and Space Mission Design. m/s. 9. Unknown parameter
|coauthors=ignored (|author=suggested) (bantuan) (16MB) - ^ Leonhard Euler, De motu rectilineo trium corporum se mutuo attrahentium (1765)
- ^ (Perancis) Lagrange, Joseph-Louis (1867–92). "Tome 6, Chapitre II: Essai sur le problème des trois corps". Oeuvres de Lagrange. Gauthier-Villars. m/s. 229–334.
- ^ Cornish, Neil J. "The Lagrangian Points" (PDF). Department of Physics, Bozeman Campus, Montana State University, USA. Diarkibkan daripada yang asal (PDF) pada 2015-09-07. Dicapai pada 29 July 2011.
- ^ Farquhar, R. W.: "The Control and Use of Libration-Point Satellites", Ph.D. Dissertation, Dept. of Aeronautics and Astronautics, Stanford University, Stanford, CA, 1968
- ^ Angular size of the Sun at 1 AU + 930000 miles: 31.6', angular size of Earth at 930000 miles: 29.3'
- ^ "Herschel Space Telescope Shut Down For Good, ESA Announces".
- ^ Lakdawalla, Emily (14 June 2012). "Chang'E 2 has departed Earth's neighborhood for.....asteroid Toutatis!?". Dicapai pada 15 Jun 2012.
- ^ "Update on yesterday's post about Chang'E 2 going to Toutatis". Planetary Society. 15 June 2012. Dicapai pada 26 June 2012.
- ^ "MISSION COMPLETE! WMAP FIRES ITS THRUSTERS FOR THE LAST TIME".
- ^ Zegler, Frank (2010-09-02). "Evolving to a Depot-Based Space Transportation Architecture" (PDF). AIAA SPACE 2010 Conference & Exposition. AIAA. m/s. 4. Diarkibkan daripada yang asal (PDF) pada 2012-03-09. Dicapai pada 2011-01-25.
L2 is in deep space far away from any planetary surface and hence the thermal, micrometeoroid, and atomic oxygen environments are vastly superior to those in LEO. Thermodynamic stasis and extended hardware life are far easier to obtain without these punishing conditions seen in LEO. L2 is not just a great gateway- it is a great place to store propellants. ... L2 is an ideal location to store propellants and cargos: it is close, high energy, and cold. More importantly, it allows the continuous onward movement of propellants from LEO depots thus suppressing their size and effectively minimizing the near-earth boiloff penalties.
Unknown parameter|coauthors=ignored (|author=suggested) (bantuan) - ^ Zegler, Frank; Bernard Kutter (2010-09-02). "Evolving to a Depot-Based Space Transportation Architecture" Diarkibkan 2012-03-09 di Wayback Machine. AIAA SPACE 2010 Conference & Exposition. AIAA. p. 4. Retrieved 2011-08-30. "We can create an energy savings account by moving propellant to the earth-moon Lagrange points—especially L2. Located 60,000 km beyond the Moon, propellant or cargo cached at L2 is very nearly at earth escape energy. It takes only a small nudge to dislodge it from Earth's gravitational grasp. This has been known for decades and L2 is often called a gateway to the solar system."
- ^ Tantardini, Marco; Fantino, Elena (2010). "Spacecraft trajectories to the L3 point of the Sun–Earth three-body problem". Celestial Mechanics and Dynamical Astronomy (Springer). Unknown parameter
|coauthors=ignored (|author=suggested) (bantuan) - ^ Space.com: First Asteroid Companion of Earth Discovered at Last
- ^ NASA—NASA's Wise Mission Finds First Trojan Asteroid Sharing Earth's Orbit
- ^ "List Of Neptune Trojans". Minor Planet Center. Diarkibkan daripada yang asal pada 2011-08-24. Dicapai pada 2010-10-27. Unknown parameter
|deadurl=ignored (bantuan)


![{\displaystyle r\approx R{\sqrt[{3}]{\frac {M_{2}}{3M_{1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1175643479ba922598c78a6d4dfcf7fff160bfe7)




