Punca kuasa dua untuk nombor 2

Punca kuasa dua adalah sama dengan hipotenus bagi segi tiga tegak yang kakinya mempunyai panjang 1.

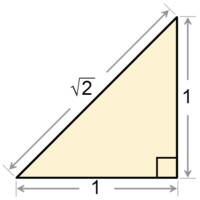
Punca kuasa 2, juga dikenali sebagai pemalar Pythagoras, sering ditulis sebagai

${\sqrt {2}},$

merupakan nombor nyata yang positif, yang apabila didarabkan dengan nilai itu sendiri akan mendapatkan nombor 2. Nilai berangkanya berhampiran 65 tempat titik perpuluhan ialah:

1.41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799.

Punca kuasa 2 merupakan nombor tak nisbah yang pertama diketahui. Secara geometri, ia merupakan kepanjangan pepenjuru merentasi segi empat sama dengan sisinya mempunyai kepanjangan 1 unit; ini mengikut teorem Pythagoras. Bagi pengiraan asas tanpa fungsi punca kuasa, penganggaran ${\tfrac {99}{70}}$ bagi punca kuasa dua lebih elok berbanding penganggaran ${\tfrac {22}{7}}$ bagi pi, yang merupakan nombor tak nisbah paling lazim digunakan.

Senarai nomobor - Nombor tak nisbah γ - ζ(3) - ${\sqrt {2}}$ - √3 - √5 - φ - α - e - π - δ
Perduaan	1.0110101000001001111...
Perpuluhan	1.4142135623730950488...
Perenambelasan	1.6A09E667F3BCC908B2F...
Pecahan lanjar	$1+{\frac {1}{2+{\frac {1}{2+{\frac {1}{2+{\frac {1}{\ddots }}}}}}}}$

Nisbah peraknya ialah

$1+{\sqrt {2}}.\,$

History

Tanah liat Babylon YBC 7289 dengan catatan.
(Imej oleh Bill Casselman)

Tablet tanah liat Babylon YBC 7289 (kk. 1800–1600 SM) memberikan anggaran ${\sqrt {2}}$ dalam bentuk perenam-puluhan, iaitu lebih kurang bentuk enam perpuluhan:

$1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}=1.41421{\overline {296}}.$

Anggaran awal yang hampir lain bagi nombor ini diberi dalam teks matematik India purba, Sulbasutra (kk. 800–200 SM) seperti berikut: Tambahkan panjang [sisi] dengan sepertiganya dan sepertiga ini dengan seperempatnya kurang sepertiga-puluh-empat bagi seperempat itu. Itu ialah,

$1+{\frac {1}{3}}+{\frac {1}{3\cdot 4}}-{\frac {1}{3\cdot 4\cdot 34}}={\frac {577}{408}}\approx 1.414215686.$

Anggaran India purba ini merupakan jujukan ketujuh bagi anggaran tepat untuk jujukan nombor Pell, yang boleh diterbitkan dari kembangan pecahan lanjar untuk ${\sqrt {2}}.$

Penemuan bagi nombor tak nisbah sering menyumbang kepada Hippasus of Metapontum Pythagoras, yang memperkenalkan bukti ketidak nisbahan (hampir kepada geometri) untuk punca kuasa 2. Menurut lagenda, Pythagoras percaya dalam kemutlakan nombor-nombor dan tidak dapat menerima nombor tak nisbah. Dia tidak dapat memalsukannya melalui logik, tetapi kepercayaannya tidak dapat menerima kewujudan nombor tak nisbah, maka dia menghukum Hippasus untuk mati lemas. [1] Lagenda lain menyatakan yang dilemaskan Hippasus oleh pengikut Pythagoras [2], atau dihalau dari golongan itu. [3]

Computation algorithm

Banyak olgoritma yang membuat penganggaran punca kuasa 2, sama ada dalam pernyataan nisbah integer atau dalam bentuk perpuluhan. Algoritma paling biasa bagi kes ini, sama ada menggunakannya dalam banyak komputer atau mesin pengira, adalah kaedah Babylon bagi pengiraan punca kuasa 2 yang merupakan salah satu daripada kaedah mengira punca kuasa. Perkara itu adalah seperti berikut:

Pertama, ambil mana-mana tekaan, $F_{0}$; tekaan itu tidak penting kerana tekaan itu hanya mempengaruhi berapa banyak lelaran yang diperlukan untuk mencapai anggaran penghampiran bagi ketepatan tertentu. Kemudian, dengan menggunakan tekaan itu, lelarkannya menerusi pengiraan rekursif tersebut:

$F_{n+1}={\frac {F_{n}+{\frac {2}{F_{n}}}}{2}}.$

Lebih banyak lelaran dalam algortma ini (iaitu banyak pengiraan dilakukan dan "n" lebih besar), lebih elok anggaran punca kuasa 2 dapat dicapai.

Nilai √2 dikira hingga 137,438,953,444 tempat perpuluhan oleh pasukan Yasumasa Kanada pada 1997.

Pada Februari 2006, rekod pengiraan √2 telah diganti dengan penggunaan komputer rumah. Shigeru Kondo mengira hingga 200,000,000,000 tempat perpuluhan dalam lebih kurang 13 hari dan 14 jam menggunakan 3.6GHz PC yang mempunyai 16GB ingatan.

Dalam banyak-banyak pemalar dengan kembangan perpuluhan tak berulang, hanya π telah dikira dengan lebih tepat. [4]