Keratan kon
Dalam matematik, keratan kon (Jawi: كراتن كون) ialah lokus dari semua titik yang membentuk lengkungan dua-dimensi, yang terbentuk oleh keratan sebuah kon dengan sebuah bidang. Tiga jenis lengkungan yang dapat terjadi ialah parabola, elips, dan hiperbola. Apollonius dari Perga ialah ahli matematik Yunani yang pertama mempelajari keratan kon secara sistematik pada awal abad ke-2 SM.
Geometri[sunting | sunting sumber]
Dalam memahami geometri keratan kon, sebuah kon dianggap memiliki dua kulit yang terbentang sehingga tidak berhingga di kedua-dua arah. Satu rosotan ialah sebuah garis yang dapat dibuat melalui kulit kon, dan semua rosotan saling berpotongan di satu titik yang disebut verteks kon.
Jenis-jenis keratan kon[sunting | sunting sumber]
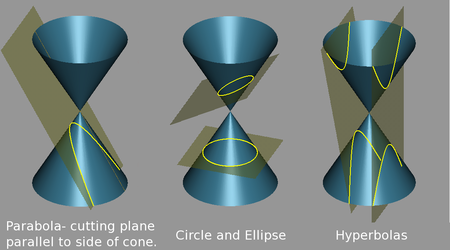
Jika sebuah bidang keratan kon sejajar dengan satu dan hanya satu rosotan, maka keamatannya ialah parabola. Jika bidang keamatan sejajar dengan dua rosotan, maka keratannya akan memotong kedua-dua kulit dan membentuk sebuah hiperbola. Sebuah elips terjadi jika bidang keamatan tidak sejajar dengan rosotan mana-mana pun. Bulatan ialah sejenis daripada elips, yang terbentuk jika bidang keratan memotong semua rosotan dan tegak lurus paksi kon.
Hal kemerosotan[sunting | sunting sumber]
Hal-hal kemerosotan terjadi jika bidang-bidang pengamatan melalui verteks kon. Keamatan-keamatan dapat berupa titik, garis lurus, dan dua garis lurus yang saling berpotongan. Sebuah titik terjadi jika hal pengamatan melalui verteks kon namun tidak memotong rosotan mana-mana pun. Hal ini merupakan elips yang termerosot. Jika bidang pengamatan melalui verteks kon, dan hanya satu kemerosotan, maka yang terjadi ialah sebuah garis lurus, dan merupakan parabola yang termerosot. Sebuah hiperbola termerosot terjadi jika bidang keamatan melalui verteks kon dan dua rosotan sehingga memberikan dua garis lurus yang saling berpotongan.
Geometri koordinat[sunting | sunting sumber]
Secara geometri koordinat, keratan kon dapat didefinisikan sebagai:
tempat kedudukan titik-titik pada sebuah bidang, sedemikian, sehingga jarak titik-titik tersebut ke sebuah titik tetap F (yang disebut fokus) memiliki nisbah yang malar terhadap jarak titik-titik tersebut ke sebuah garis tetap L (disebut direktriks) yang tidak mengandungi F[1].

Nisbah yang malar tersebut disebut kesipian, dilambangkan dengan e, dan merupakan bilangan bukan-negatif. Untuk e = 0, keratan kon tersebut ialah bulatan, 0 < e < 1 sebuah elips, e = 1 sebuah parabola, dan e > 1 sebuah hiperbola.
Sistem koordinat Cartes[sunting | sunting sumber]
Dalam Sistem koordinat Cartes, grafik dari persamaan kuadrati dengan dua pemboleh ubah selalu menghasilkan keratan kon, dan semua keratan kon dapat dihasilkan melalui cara ini.
Jika terdapat persamaan dengan bentuk:
maka:
- Jika h2 = ab, persamaan ini menghasilkan parabola.
- Jika h2 < ab, persamaan ini menghasilkan elips.
- Jika h2 > ab, persamaan ini menghasilkan hiperbola.
- Jika a = b and h = 0, persamaan ini menghasilkan bulatan.
- Jika a + b = 0, persamaan ini menghasilkan hiperbola persegi.
Rujukan[sunting | sunting sumber]
- ^ Leithold, Louis (1981). "13". The Calculus with Analytic Geometry. New York: Harper & Row, Publisher, Inc. m/s. 657. ISBN 0-06-043935-1.

