Pekali Gini

Pekali Gini adalah suatu ukuran penyerakan statistik dikembangkan oleh ahli statistik dan ahli sosiologi Itali Corrado Gini dan menerbit dalam karya 1912nya "Keberubahan dan Keberubah-ubahan" (Itali: Variabilità e mutabilità).[1][2]
Pekali Gini adalah ukuran ketidaksamaan edaran, nilai 0 menyatakan kesamaan jumlah dan nilai 1 ketidaksamaan maksimum. Ini telah menemukan permohonan dalam kajian ketidaksamaan dalam bidang beragam seperti sosiologi, ekonomi, sains penjagaan kesihatan, ekologi, kimia, kejuruteraan dan pertanian.[3]
Hal ini biasanya digunakan sebagai ukuran ketidaksamaan dari pendapatan atau kekayaan.[4] Di seluruh dunia, pekali Gini untuk rentang pendapatan daripada 0.23 (Sweden) ke 0.70 (Namibia) walaupun tidak setiap negara telah dinilai.
Takrifan[sunting | sunting sumber]

Graf menunjukkan bahawa Gini yang sama dengan daerah yang ditandai 'A' ditandai dibahagikan dengan jumlah daerah 'A' dan 'B' (iaitu, Gini = A / (A + B)). Hal ini juga sama dengan 2 * A, sebagai A + B = 0.5 (kerana skala paksi daripada 0 ke 1).
Pekali Gini biasanya ditakrifkan matematik berasas di lengkung Lorenz, yang plot perkadaran dari jumlah keseluruhan pendapatan penduduk (paksi y) yang secara kumulatif diperolehi oleh bahagian bawah% x penduduk (lihat diagram). Garis di 45 darjah kesamaan yang sempurna sehingga merupakan pendapatan. Pekali Gini kemudian boleh dianggap sebagai nisbah dari daerah yang terletak di antara garis persamaan dan kurva Lorenz (ditandakan 'A' dalam carta) ke atas wilayah total di bawah garis kesetaraan (ditandakan 'A' dan 'B' dalam carta), iaitu G = A / (A + B).
Pekali Gini boleh berkisar dari 0 hingga 1, kadang-kadang didarabkan dengan 100 berkisar antara 0 dan 100. Sebuah pekali Gini yang rendah menunjukkan edaran yang lebih sama, dengan 0 yang sesuai untuk menyelesaikan persamaan, sedangkan pekali Gini yang lebih tinggi menunjukkan edaran yang lebih merata, dengan 1 berkaitan untuk menyelesaikan ketidaksamaan. Untuk menjadi sah dikira, tidak ada barang negatif dapat diedarkan. Jadi, jika pekali Gini yang digunakan untuk menggambarkan pendapatan rumah tangga ketidaksamaan, maka tidak ada rumah tangga boleh mempunyai pendapatan negatif. Apabila digunakan sebagai ukuran ketidaksamaan pendapatan, masyarakat yang paling tidak sama akan menjadi salah satu di mana satu orang menerima 100% dari jumlah keseluruhan pendapatan dan orang-orang yang tersisa tidak menerima (G = 1); dan masyarakat yang paling sama akan menjadi salah satu yang setiap orang menerima pendapatan yang sama (G = 0).
Beberapa merasa lebih intuitif (dan itu adalah matematik setara) untuk memikirkan pekali Gini sebagai setengah dari relatif perbezaan bererti. Perbezaan rata-rata adalah rata-rata mutlak perbezaan antara dua item yang dipilih secara rawak dari suatu populasi, dan perbezaan rata-rata relatif adalah perbezaan bererti dibahagikan dengan rata-rata, untuk menormalkan untuk skala.
Perhitungan[sunting | sunting sumber]
Indeks Gini ditakrifkan sebagai nisbah dari daerah pada [kurva [Lorenz]] diagram. Jika kawasan antara garis persamaan yang sempurna dan kurva Lorenz adalah A, dan kawasan di bawah kurva Lorenz adalah B, maka indeks Gini A / (A + B). Kerana A + B = 0.5, indeks Gini, G = A / (0.5) = 2A = 1-2B. Jika kurva Lorenz diwakili oleh fungsi Y = L (X), nilai B boleh didapati dengan integrasi dan:
Dalam beberapa kes, persamaan ini dapat diterapkan untuk menghitung pekali Gini tanpa rujukan terus ke kurva Lorenz. Sebagai contoh:
- Untuk seragam penduduk pada nilai-nilai'y'< sub> i </ sub >,' i = 1 untuk n , diindeks dalam penurunan bukan urutan ( yi ≤ yi+1):
- Ini mungkin dimudahkan untuk:
- Untuk kebarangkalian fungsi diskrit f (y ), di mana yi, i = 1 to n, are the points with nonzero probabilities and which are indexed in increasing order ( yi < yi+1):
- where
- dan
- Untuk fungsi edaran kumulatif F (y ) iaitu sesepenggal terdiferensialkan, memiliki bererti μ, dan sifar untuk semua negatif nilai y :
- Kerana pekali Gini adalah setengah perbezaan bererti relatif, juga boleh dikira dengan menggunakan rumus untuk selisih rata-rata relatif. Untuk sampel acak S yang terdiri dari nilai-nilai 'y'< sub> i </ sub>,' i = 1 untuk'n, yang diindeks dalam urutan bukan menurun ( yi ≤ yi+1), the statistic:
- adalah sebuah penganggar tekal penduduk pekali Gini, tetapi tidak, secara umum, bias. Seperti, G, G (S) mempunyai bentuk yang lebih sederhana:
- .
Tidak ada suatu statistik sampel yang secara umum merupakan estimator yang tidak bias daripada penduduk pekali Gini, seperti perbezaan relatif bererti.
Untuk beberapa bentuk berfungsi, indeks Gini boleh dikira secara jelas. Sebagai contoh, jika y'mengikuti edaran lognormal dengan standard deviasi log sebanyak , then where adalah edaran fungsi kumulatif dari edaran biasa piawai.
Kadang-kadang kurva Lorenz turun tidak diketahui, dan hanya nilai-nilai pada interval tertentu diberikan. Dalam hal ini, pekali Gini boleh didekati dengan menggunakan pelbagai teknik untuk interpolasi nilai-nilai yang hilang dari kurva Lorenz. Jika ( X k , Yk ) adalah dikenali mata pada kurva Lorenz, dengan X k diindeks dalam rangka meningkatkan ( X k - 1 < X k ), sehingga:
- Xk adalah perkadaran dijaga dari pembolehubah penduduk, untuk k = 0,...,n, dengan X0 = 0, Xn = 1.
- Yk adalah perkadaran dijaga dari pembolehubah pendapatan, untuk k = 0,...,n, dengan Y0 = 0, Yn = 1.
- Yk harus diindeks urutan bukan penurunan (Y k>Yk-1)
Jika lengkung Lorenz adalah didekati pada selang masing-masing sebagai garis antara titik berturut-turut, maka daerah B dapat didekati dengan segi empat yang dua sisinya sejalan dan:
adalah pendekatan yang dihasilkan untuk mendapatkan hasil G. lebih tepat boleh diperolehi dengan menggunakan kaedah lain untuk anggaran daerah B, seperti mendekati lengkung Lorenz dengan kuadrat fungsi di seberang pasang selang , atau membina pendekatan tepat halus dengan fungsi edaran yang mendasari yang berpadanan dengan data yang dikenali. Jika penduduk mean dan batas nilai untuk setiap selang juga dikenali, ini dapat juga sering digunakan untuk meningkatkan ketepatan pendekatan tersebut.
Pekali Gini dikira dari sampel adalah statistik dan standard error, atau selang keyakinan bagi penduduk pekali Gini, harus dilaporkan. Ini boleh dikira dengan menggunakan teknik Bootstrap tapi yang dicadangkan telah matematik rumit dan pengkomputeran berat bahkan dalam era komputer cepat. Ogwang (2000) membuat proses yang lebih efisien dengan menyiapkan suatu "model muslihat kemerosotan" di mana pendapatan dalam sampel ini adalah peringkat dengan pendapatan terendah diperuntukkan peringkat 1. Model kemudian menyatakan kedudukan (pembolehubah bergantung) sebagai jumlah dari konstan A dan suatu istilah silap muzik yang variannya berbanding terbalik dengan yk;
Ogwang menunjukkan bahawa G dapat dinyatakan sebagai fungsi dari kuadrat terkecil tertimbang anggaran konstan A dan yang ini boleh digunakan untuk mempercepat perhitungan estimasi berlipat untuk standard error. Giles (2004) berpendapat bahawa kesalahan piawai dari anggaran A boleh digunakan untuk mendapatkan bahawa dari estimasi G secara langsung tanpa menggunakan berlipat sama sekali. Kaedah ini hanya memerlukan penggunaan regresi kuasa dua terkecil selepas menempah data sampel. Keputusan baik berbanding dengan anggaran dari berlipat dengan perjanjian meningkatkan dengan peningkatan saiz sampel. Kertas menjelaskan kaedah ini boleh didapati di sini: http://web.uvic.ca/econ/ewp0202.pdf
Namun sejak saat itu telah berpendapat bahawa hal ini bergantung pada andaian model tentang pengedaran kesalahan (Ogwang 2004) dan kebebasan istilah kesalahan (Reza & Gastwirth 2006) dan bahawa andaian-andaian ini seringkali tidak berlaku untuk set data yang nyata. Oleh itu mungkin lebih baik untuk tetap dengan kaedah berlipat seperti yang dicadangkan oleh Yitzhaki (1991) dan Karagiannis dan Kovacevic (2000). Perdebatan terus berlanjut.
Pekali Gini boleh dikira jika anda tahu mean dari edaran, jumlah orang (atau persentil), dan pendapatan setiap orang (atau persentil). Princeton ahli pembangunan ekonomi Angus Deaton (1997, 139) menyederhanakan perhitungan Gini untuk satu formula yang mudah:
mana u bererti pendapatan penduduk, P i</ sub> adalah peringkat pendapatan P i orang, dengan pendapatan X, seperti yang orang terkaya menerima peringkat 1 dan peringkat termiskin N. ini berkesan memberikan bobot yang lebih tinggi kepada orang miskin dalam pengagihan pendapatan, yang membolehkan Gini untuk memenuhi Prinsip Transfer.
Indeks ketidaksamaan diumumkan[sunting | sunting sumber]
- Lihat juga: Indeks entropi diumumkan
Pekali Gini dan indeks mengurangkan jurang piawai untuk bentuk umum. Sempurna kesamaan-tidak adanya ketidaksamaan-wujud bila dan hanya jika nisbah ketidaksamaan, , sama dengan 1 untuk semua unit j dalam jumlah penduduk beberapa, misalnya, wujud kesamaan pendapatan yang sempurna ketika semua pendapatan orang sama dengan pendapatan purata , sehingga untuk semua orang). Saiz ketidaksamaan, kemudian, adalah saiz penyimpangan purata dari 1, semakin besar deviasi rata-rata, semakin besar ketidaksamaan tersebut. Berdasarkan pengamatan ini indeks ketidaksamaan mempunyai bentuk umum:[5]
di mana pj menimbang unit mengikut bahagian jumlah penduduk mereka, dan f(rj) adalah fungsi dari masing-masing penyimpangan rj unit dari 1, titik kesamaan. Pemahaman ini indeks ketidaksamaan umum adalah bahawa indeks ketidaksamaan berbeza kerana mereka menggunakan fungsi yang berbeza dari jarak nisbah ketidaksamaan (rj) dari 1.
Pekali Gini edaran pendapatan[sunting | sunting sumber]
- Lihat juga: Senarai negara mengikut kesamaan pendapatan
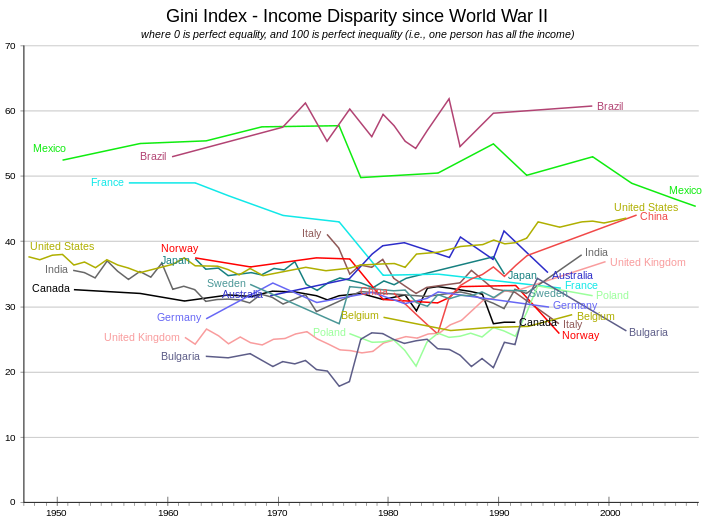
Sementara negara-negara Eropah maju dan Kanada lebih mirip kepada mempunyai indeks Gini antara 24 dan 36, Amerika Syarikat dan Mexico indeks Gini keduanya di atas 40, menunjukkan bahawa Amerika Syarikat dan Mexico mempunyai jurang yang lebih besar. Menggunakan Gini boleh membantu menghitung perbezaan di kesejahteraan dan pampasan dasar dan falsafah. Namun harus diingat bahawa pekali Gini boleh menyesatkan apabila digunakan untuk membuat perbandingan politik antara negara-negara besar dan kecil (lihat kritik bahagian).
Indeks Gini untuk seluruh dunia telah dijangka oleh pelbagai pihak menjadi antara 56 dan 66.[6][7]
Indeks Gini gaji AS dari masa ke masa[sunting | sunting sumber]
Indeks Gini untuk Amerika Syarikat di pelbagai waktu, menurut Biro Bancian AS:[8][9][10]
- 1929: 45.0 (dianggarkan)
- 1947: 37.6 (dianggarkan)
- 1967: 39.7 (tahun pertama dilaporkan)
- 1968: 38.6 (indeks paling rendah dilaporkan)
- 1970: 39.4
- 1980: 40.3
- 1990: 42.8
- (Perhitungan semula dibuat pada tahun 1992 menambah bergeser ke atas yang signifikan untuk nilai nanti)
- 2000: 46.2
- 2005: 46.9
- 2006: 47.0 (indeks tertinggi dilaporkan)
- 2007: 46.3
- 2008: 46.69
- 2009: 46.8
Indeks Gini EU[sunting | sunting sumber]
Pada tahun 2005 indeks Gini untuk Kesatuan Eropah dijangka mencapai 31.[11]
Keuntungan dan kelemahan[sunting | sunting sumber]
Templat:Proandconlist Templat:Section OR
Keuntungan pekali Gini sebagai ukuran ketidaksamaan[sunting | sunting sumber]
Keuntungan utama pekali Gini itu bahawa itu adalah ukuran ketidaksamaan melalui suatu analisis nisbah. Hal ini membuat mudah diterjemahkan, dan mengelakkan rujukan mengikut rata-rata statistik atau kedudukan tidak representatif dari sebahagian besar penduduk, seperti pendapatan tiap kapita atau keluaran dalam negara kasar. Kesederhanaan Gini membuatnya mudah digunakan untuk perbandingan di pelbagai negara dan juga membolehkan perbandingan pengedaran pendapatan di seluruh kumpulan yang berbeza dan negara-negara, misalnya pekali Gini untuk kawasan bandar berbeza dari kawasan luar bandar di banyak negara (walaupun tidak dalam Amerika Syarikat). Seperti mengukur masa-based, pekali Gini boleh digunakan untuk membandingkan pengedaran pendapatan dari masa ke masa, sehingga adalah mungkin untuk melihat apakah ketidaksamaan semakin meningkat atau menurun bergantung pada pendapatan mutlak. Koefisien Gini memenuhi empat prinsip yang disarankan menjadi penting:[12]
- Ketanpanamaan: tidak peduli siapa yang berpendapatan tinggi dan rendah.
- Skala kebebasan: pekali Gini tidak mempertimbangkan saiz ekonomi, cara diukur, atau apakah itu negara kaya atau miskin rata-rata.
- Kebebasan penduduk: tidak peduli seberapa besar penduduk negara ini.
- Prinsip pemindahan: jika pendapatan (kurang dari perbezaannya), akan dipindahkan dari orang kaya kepada orang miskin edaran yang dihasilkan lebih sama.
Kelemahan dari pekali Gini sebagai saiz ketidaksamaan[sunting | sunting sumber]
Kelemahan Gini sebahagian besar terletak di alam relatif: Ini kehilangan maklumat tentang pendapatan nasional dan peribadi mutlak. Negara-negara mungkin mempunyai pekali Gini identik, namun sangat berbeza dalam kekayaan. keperluan asas mungkin sama (tersedia untuk semua) di negara kaya, sementara di negara miskin, bahkan keperluan asas yang tidak merata sedia. Selain itu, Gini tidak membahas penyebab: kesamaan pendapatan mungkin mencerminkan perbezaan dalam peluang, atau kemampuan. Sebagai contoh, beberapa negara mungkin mempunyai struktur kelas sosial yang menyajikan halangan untuk mobiliti ke atas, beberapa orang mungkin mempunyai kemampuan lebih dari yang lain. Dengan mengukur ketimpangan pendapatan, Gini mengabaikan perbezaan kecekapan penggunaan pendapatan rumah tangga. Dengan mengabaikan kekayaan (kecuali kerana memberi sumbangan pada pendapatan) Gini boleh mencipta paparan ketimpangan ketika orang berbanding berada pada tahap yang berbeza dalam hidup mereka. negara-negara kaya (misalnya Sweden) dapat tampil lebih sama, namun memiliki koefisien Gini yang tinggi untuk kekayaan (misalnya 77% dari nilai saham yang dimiliki oleh rumah tangga dipegang oleh hanya 5% dari rumah tangga saham Sweden).[13] These factors are not assessed in income-based Gini.
Gini mempunyai beberapa ciri-ciri matematik negatif. Sebagai contoh, set orang yang berbeza tidak dapat dipuratakan untuk mendapatkan pekali Gini dari semua orang di set: jika pekali Gini itu harus dikira untuk setiap orang itu akan selalu sifar. Untuk sebuah negara, besar ekonomi pelbagai, yang jauh lebih tinggi akan dikira pekali bagi negara secara keseluruhan daripada akan dikira untuk masing-masing wilayah. (Koefisien biasanya diterapkan untuk diukur ukuran dasar pendapatan daripada tempatan kuasa beli, cenderung meningkatkan dikira pekali di seluruh wilayah yang lebih besar.)
Seperti halnya untuk setiap saiz tunggal pengedaran, ekonomi dengan pendapatan yang sama dan pekali Gini masih boleh mempunyai pengedaran pendapatan yang sangat berbeza. Ini hasil dari berbeza bentuk kurva Lorenz. Sebagai contoh, pertimbangkan sebuah masyarakat di mana setengah dari individu-individu tidak mempunyai keuntungan dan setengah yang lain bersama semua pendapatan sama (iaitu yang kurva Lorenz adalah linier dari (0,0) sampai (0.5,0) dan kemudian linear untuk (1,1) ). Seperti mudah dikira, masyarakat ini mempunyai pekali Gini 0,5 - sama seperti yang dari masyarakat di mana 75% dari orang ditanggung bersama 25% dari pendapatan sedangkan 25% sisanya ditanggung bersama 75% (iaitu kurva Lorenz yang linier dari ( 0,0) ke (0.75,0.25) dan kemudian linear untuk 1,1 ()).
- Terlalu sering hanya pekali Gini dikutip tanpa menjelaskan perkadaran Taburan nilai yang digunakan untuk pengukuran. Seperti dengan pekali ketimpangan yang lain, pekali Gini dipengaruhi oleh granularity pengukuran. Sebagai contoh, lima 20% Taburan (granularity rendah) biasanya akan menghasilkan pekali Gini yang lebih rendah daripada dua puluh 5 Taburan% (granularity quality) diambil dari edaran yang sama. Ini adalah masalah yang sering dijumpai dengan pengukuran.
- Penjagaan harus diambil dalam menggunakan pekali Gini sebagai saiz egalitarianisme, kerana benar saiz dispersi pendapatan. Sebagai contoh, jika dua negara yang sama egaliter mengejar dasar imigresen yang berbeza, negara menerima perkadaran yang lebih tinggi rendah-pendapatan atau migran miskin akan dinilai kurang sama (keuntungan yang lebih tinggi pekali Gini).
Memperluas tentang pentingnya langkah-langkah hidup-span, pekali Gini sebagai anggaran-titik persamaan pada waktu tertentu, mengabaikan perubahan hidup span pendapatan. Biasanya, peningkatan kadar ahli muda atau tua dari masyarakat akan mendorong perubahan nyata dalam kesetaraan. Oleh itu, faktor-faktor seperti pengedaran umur dalam populasi dan mobiliti dalam kelas pendapatan boleh mencipta paparan persamaan pembezaan ketika tidak ada dengan mempertimbangkan kesan akaun demografi. Jadi ekonomi tertentu mungkin mempunyai pekali Gini yang lebih tinggi pada satu titik masa berbanding dengan yang lain, sedangkan pekali Gini dikira atas pendapatan seumur hidup individu sebenarnya lebih rendah daripada ekonomi rupanya lebih sama (pada titik tertentu dalam waktu) itu.[14] Essentially, what matters is not just inequality in any particular year, but the composition of the distribution over time.
Masalah umum pengukuran[sunting | sunting sumber]
- Edaran pendapatan Membandingkan antara negara-negara mungkin sukar kerana manfaat sistem tersebut mungkin berbeza. Sebagai contoh, beberapa negara memberikan manfaat dalam bentuk wang sementara yang lain memberikan kupon makanan, yang mungkin tidak dikira oleh beberapa ahli ekonomi dan penyelidik sebagai pendapatan dalam kurva Lorenz dan kerananya tidak diambil kira dalam pekali Gini. Pendapatan di Amerika Syarikat adalah dikira sebelum manfaat, sementara di Perancis itu dikira selepas manfaat, yang dapat memimpin Amerika Syarikat untuk tampil agak lebih merata vis-a-vis Perancis. Dalam contoh lain, Kesatuan Soviet diukur untuk memiliki ketidaksamaan pendapatan relatif tinggi: oleh beberapa anggaran, pada akhir tahun 1970, pekali Gini penduduk bandar syarikat adalah sebagai quality 0.38,[15] yang lebih tinggi daripada negara-negara Barat saat ini. Jumlah ini tidak akan mencerminkan manfaat yang diterima oleh warga Soviet yang tidak menghasilkan wang untuk pengukuran, yang mungkin termasuk penjagaan anak untuk anak-anak pendidikan berusia dua bulan, dasar, menengah dan tinggi, rawatan perubatan cradle-to-kubur, dan banyak disubsidi atau disediakan perumahan. Dalam contoh ini, perbandingan yang lebih tepat antara tahun 1970-an Kesatuan Soviet dan negara-negara Barat mungkin memerlukan satu untuk menetapkan nilai kewangan untuk seluruh ganjaran - tugas yang sukar kerana tidak adanya pasaran bebas. Masalah serupa muncul setiap kali perbandingan antara ekonomi pasaran bebas murni dan sebahagian ekonomi sosialis yang dicuba. Manfaat dapat mengambil berbagai bentuk dan tak terduga: contohnya, pengilang minyak utama seperti Venezuela dan Iran memberikan manfaat tidak langsung kepada warganya dengan subsidi harga runcit petrol.
- Demikian pula, dalam beberapa masyarakat orang mungkin mempunyai pendapatan yang signifikan dalam bentuk selain wang, misalnya melalui pertanian saraan hidup atau tukar barang. Seperti manfaat bukan-kewangan, nilai pendapatan ini sukar untuk diukur. kuantifikasi yang berbeza dari pendapatan yang berbeza akan menghasilkan pekali Gini.
- Mengukur akan memberikan hasil yang berbeza ketika diterapkan kepada individu-individu daripada rumah tangga. Ketika penduduk yang berbeza tidak diukur dengan takrif yang tekal, perbandingan tidak bermakna.
- Sebagai untuk semua statistik, mungkin ada kesalahan sistematik dan rawak dalam data. Maksud pekali Gini menurun sebagai data menjadi kurang tepat. Selain itu, negara-negara dapat mengumpul data yang berbeza, sehingga sukar untuk membandingkan statistik antara negara.
Sebagai salah satu akibat dari kritikan, di samping atau di dalam persaingan dengan mengukur pekali Gini entropi yang sering digunakan (misalnya Indeks Theil dan Indeks Atkinson). Langkah-langkah ini cuba untuk membandingkan pengedaran sumber daya oleh agen cerdas dalam pasaran dengan entropi maksimum Rawak edaran, yang akan terjadi jika agen bertindak seperti zarah non-cerdas dalam sistem tertutup berikut undang-undang fizik statistik.
Risiko kredit[sunting | sunting sumber]
Koefisien Gini juga biasa digunakan untuk pengukuran daya perselisihan sistem kadaran dalam pengurusan risiko kredit.
Kekuatan diskriminasi merujuk pada kemampuan risiko kredit model untuk membezakan antara pelanggan mungkir dan bukan-mungkir. Rumus di atas boleh digunakan untuk model final dan juga di peringkat model faktor individu, untuk mengukur kekuatan diskriminasi faktor individu. Hal ini sebagai akibat dari terlalu banyak pelanggan yang mangkir tidak jatuh ke dalam misalnya mata lebih rendah skala faktor mempunyai 10 titik skala dan 30% dari pelanggan yang mangkir tidak sedang diberi titik terendah yang sedia misalnya 0 atau negatif mata. Hal ini menunjukkan bahawa faktor tersebut berfungsi secara kontra-intuitif dan akan memerlukan penyelidikan lebih lanjut pada tahap pembangunan model.[16]
Kegunaan lain[sunting | sunting sumber]
Walaupun pekali Gini yang paling popular di bidang ekonomi, boleh secara teori diterapkan dalam setiap bidang ilmu yang mempelajari pengedaran. Misalnya, dalam ekologi pekali Gini telah digunakan sebagai ukuran keanekaragaman hayati, di mana perkadaran kumulatif spesies diplot terhadap perkadaran kumulatif individu.[17] In health, it has been used as a measure of the inequality of health related quality of life in a population.[18] Dalam pendidikan, telah digunakan sebagai ukuran ketidaksamaan universiti.[19] Dalam bidang kimia telah digunakan untuk menyatakan selektivitas protein inhibitor kinase terhadap panel kinase.[20] In engineering, it has been used to evaluate the fairness achieved by Internet routers in scheduling packet transmissions from different flows of traffic.[21] Dalam statistik, membina pokok keputusan, digunakan untuk mengukur kemurnian node anak mungkin, mengikut tujuan untuk memaksimumkan kemurnian rata-rata dua node anak ketika pembahagian, dan telah dibandingkan mengikut langkah-langkah kesamaan lain.[22]
Lihat juga[sunting | sunting sumber]
Rujukan[sunting | sunting sumber]
- ^ Gini, C. (1912) (Itali: Variabilità e mutabilità (Variability and Mutability), C. Cuppini, Bologna, 156 pages. Reprinted in Memorie di metodologica statistica (Ed. Pizetti E, Salvemini, T). Rome: Libreria Eredi Virgilio Veschi (1955).
- ^ Gini, C (1909) Concentration and dependency ratios (in Italian). English translation in Rivista di Politica Economica, 87 (1997), 769-789.
- ^ Sadras, V.O., Bongiovanni, R., 2004. Use of Lorenz curves and Gini coefficients to assess yield inequality within paddocks. Field Crops Res. 90, 303-310.
- ^ Gini, C. (1936) On the Measure of Concentration with Special Reference to Income and Statistics, Colorado College Publication, General Series No. 208, 73-79.
- ^ Firebaugh, Glenn (1999). "Empirics of World Income Inequality". American Journal of Sociology. 104 (6): 1597–1630. doi:10.1086/210218.. See also Firebaugh, Glenn (2003). "Inequality: What it is and how it is measured". The New Geography of Global Income Inequality. Cambridge, MA: Harvard University Press. ISBN 0674010671. Unknown parameter
|authormask=ignored (bantuan). - ^ Bob Sutcliffe (2007). "Postscript to the article 'World inequality and globalization' (Oxford Review of Economic Policy, Spring 2004)" (PDF). Dicapai pada 13 Disember 2007. Unknown parameter
|month=ignored (bantuan) - ^ United Nations Development Programme
- ^ "Gini Ratios for Households, by Race and Hispanic Origin of Householder: 1967 to 2007". Historical Income Tables - Households. United States Census Bureau.
- ^ "Table 3. Income Distribution Measures Using Money Income and Equivalence-Adjusted Income: 2007 and 2008" (PDF). Income, Poverty, and Health Insurance Coverage in the United States: 2008. United States Census Bureau. m/s. 17.
- ^ "Income, Poverty and Health Insurance Coverage in the United States: 2009". Newsroom. United States Census Bureau.
- ^ "Monitoring quality of life in Europe - Gini index". Eurofound. 26 Ogos 2009. Diarkibkan daripada yang asal pada 1 Disember 2008. Dicapai pada 31 Mei 2011..
- ^ Ray, Debraj (1998). Development Economics. Princeton, NJ: Princeton University Press. m/s. 188. ISBN 0691017069..
- ^ (Data from the Statistics Sweden)
- ^ Blomquist, N. (1981). "A comparison of distributions of annual and lifetime income: Sweden around 1970". Review of Income and Wealth. 27 (3): 243–264. doi:10.1111/j.1475-4991.1981.tb00227.x..
- ^ Millar, James R. (1987). Politics, work, and daily life in the USSR. New York: Cambridge University Press. m/s. 193. ISBN 0521348900..
- ^ The Analytics of risk model validation [specify]
- ^ Wittebolle, Lieven (2009). "Initial community evenness favours functionality under selective stress". Nature. 458 (7238): 623–626. doi:10.1038/nature07840. PMID 19270679. Unknown parameter
|coauthors=ignored (|author=suggested) (bantuan) - ^ Asada, Yukiko (2005). "Assessment of the health of Americans: the average health-related quality of life and its inequality across individuals and groups". Population Health Metrics. 3: 7. doi:10.1186/1478-7954-3-7. PMC 1192818. PMID 16014174.
- ^ Halffman, Willem; Leydesdorff, L (2010). "Is Inequality Among Universities Increasing? Gini Coefficients and the Elusive Rise of Elite Universities". Minerva. 48 (1): 55–72. doi:10.1007/s11024-010-9141-3. PMC 2850525. PMID 20401157.
- ^ Graczyk, Piotr (2007). "Gini Coefficient: A New Way To Express Selectivity of Kinase Inhibitors against a Family of Kinases". Journal of Medicinal Chemistry. 50 (23): 5773–5779. doi:10.1021/jm070562u. PMID 17948979.
- ^ Shi, Hongyuan; Sethu, Harish (2003). "Greedy Fair Queueing: A Goal-Oriented Strategy for Fair Real-Time Packet Scheduling". Proceedings of the 24th IEEE Real-Time Systems Symposium. IEEE Computer Society. m/s. 345–356. ISBN 0-7695-2044-8.
- ^ Gonzalez, Luis (2010). "The Similarity between the Square of the Coeficient of Variation and the Gini Index of a General Random Variable". Journal of Quantitative Methods for Economics and Business Administration. 10: 5–18. ISSN 1886-516X. Unknown parameter
|coauthors=ignored (|author=suggested) (bantuan)[pautan mati kekal]
Bacaan lebih lanjut[sunting | sunting sumber]
- Amiel, Y.; Cowell, F.A. (1999). Thinking about Inequality. Cambridge. ISBN 0521466962.CS1 maint: multiple names: authors list (link)
- Anand, Sudhir (1983). Inequality and Poverty in Malaysia. New York: Oxford University Press. ISBN 0195201531.
- Brown, Malcolm (1994). "Using Gini-Style Indices to Evaluate the Spatial Patterns of Health Practitioners: Theoretical Considerations and an Application Based on Alberta Data". Social Science Medicine. 38 (9): 1243–1256. doi:10.1016/0277-9536(94)90189-9. PMID 8016689.
- Chakravarty, S. R. (1990). Ethical Social Index Numbers. New York: Springer-Verlag. ISBN 0387522743.
- Deaton, Angus (1997). Analysis of Household Surveys. Baltimore MD: Johns Hopkins University Press. ISBN 0585237875.
- Dixon, PM, Weiner J., Mitchell-Olds T, Woodley R. (1987). "Bootstrapping the Gini coefficient of inequality". Ecology. Ecological Society of America. 68 (5): 1548–1551. doi:10.2307/1939238. JSTOR 1939238.CS1 maint: multiple names: authors list (link)
- Dorfman, Robert (1979). "A Formula for the Gini Coefficient". The Review of Economics and Statistics. The MIT Press. 61 (1): 146–149. doi:10.2307/1924845. JSTOR 1924845.
- Firebaugh, Glenn (2003). The New Geography of Global Income Inequality. Cambridge MA: Harvard University Press. ISBN 0674010671.
- Gastwirth, Joseph L. (1972). "The Estimation of the Lorenz Curve and Gini Index". The Review of Economics and Statistics. The MIT Press. 54 (3): 306–316. doi:10.2307/1937992. JSTOR 1937992.
- Giles, David (2004). "Calculating a Standard Error for the Gini Coefficient: Some Further Results". Oxford Bulletin of Economics and Statistics. 66 (3): 425–433. doi:10.1111/j.1468-0084.2004.00086.x.
- Gini, Corrado (1912). "Variabilità e mutabilità" Reprinted in Memorie di metodologica statistica (Ed. Pizetti E, Salvemini, T). Rome: Libreria Eredi Virgilio Veschi (1955).
- Gini, Corrado (1921). "Measurement of Inequality of Incomes". The Economic Journal. Blackwell Publishing. 31 (121): 124–126. doi:10.2307/2223319. JSTOR 2223319.
- Giorgi, G. M. (1990). A bibliographic portrait of the Gini ratio, Metron, 48, 183-231.
- Karagiannis, E. and Kovacevic, M. (2000). "A Method to Calculate the Jackknife Variance Estimator for the Gini Coefficient". Oxford Bulletin of Economics and Statistics. 62: 119–122. doi:10.1111/1468-0084.00163.CS1 maint: multiple names: authors list (link)
- Mills, Jeffrey A.; Zandvakili, Sourushe (1997). "Statistical Inference via Bootstrapping for Measures of Inequality". Journal of Applied Econometrics. 12 (2): 133–150. doi:10.1002/(SICI)1099-1255(199703)12:2<133::AID-JAE433>3.0.CO;2-H.CS1 maint: multiple names: authors list (link)
- Modarres, Reza and Gastwirth, Joseph L. (2006). "A Cautionary Note on Estimating the Standard Error of the Gini Index of Inequality". Oxford Bulletin of Economics and Statistics. 68 (3): 385–390. doi:10.1111/j.1468-0084.2006.00167.x.CS1 maint: multiple names: authors list (link)
- Morgan, James (1962). "The Anatomy of Income Distribution". The Review of Economics and Statistics. The MIT Press. 44 (3): 270–283. doi:10.2307/1926398. JSTOR 1926398.
- Ogwang, Tomson (2000). "A Convenient Method of Computing the Gini Index and its Standard Error". Oxford Bulletin of Economics and Statistics. 62: 123–129. doi:10.1111/1468-0084.00164.
- Ogwang, Tomson (2004). "Calculating a Standard Error for the Gini Coefficient: Some Further Results: Reply". Oxford Bulletin of Economics and Statistics. 66 (3): 435–437. doi:10.1111/j.1468-0084.2004.00087.x.
- Xu, Kuan (Januari 2004). "How Has the Literature on Gini's Index Evolved in the Past 80 Years?" (PDF). Department of Economics, Dalhousie University. Dicapai pada 1 Jun 2006. Cite journal requires
|journal=(bantuan) The Chinese version of this paper appears in Xu, Kuan (2003). "How Has the Literature on Gini's Index Evolved in the Past 80 Years?". China Economic Quarterly. 2: 757–778. - Yitzhaki, S. (1991). "Calculating Jackknife Variance Estimators for Parameters of the Gini Method". Journal of Business and Economic Statistics. American Statistical Association. 9 (2): 235–239. doi:10.2307/1391792. JSTOR 1391792.
Pautan luar[sunting | sunting sumber]
- Deutsche Bundesbank: Do banks diversify loan portfolios? Diarkibkan 2008-12-18 di Wayback Machine, 2005 (on using e.g. the Gini coefficient for risk evaluation of loan portfolios)
- Forbes Article, In praise of inequality
- Measuring Software Project Risk With The Gini Coefficient Diarkibkan 2010-08-09 di Wayback Machine, an application of the Gini coefficient to software
- The World Bank: Measuring Inequality
- Travis Hale, University of Texas Inequality Project:The Theoretical Basics of Popular Inequality Measures, online computation of examples: 1A, 1B
- United States Census Bureau List of Gini Coefficients by State for Families and Households
- Article from The Guardian analysing inequality in the UK 1974 - 2006
- World Income Inequality Database Diarkibkan 2011-03-13 di Wayback Machine
- Income Distribution and Poverty in OECD Countries
- Software:
- A Matlab Inequality Package, including code for computing Gini, Atkinson, Theil indexes and for plotting the Lorenz Curve. Many examples are available.
- Free Online Calculator Diarkibkan 2012-12-04 di archive.today computes the Gini Coefficient, plots the Lorenz curve, and computes many other measures of concentration for any dataset
- Free Calculator: Online and downloadable scripts Diarkibkan 2004-10-12 di Wayback Machine (Python and Lua) for Atkinson, Gini, and Hoover inequalities
- Users of the R data analysis software can install the "ineq" package which allows for computation of a variety of inequality indices including Gini, Atkinson, Theil.
- LORENZ 2.0 is a Mathematica notebook available from C. Damgaard Diarkibkan 2011-08-07 di Wayback Machine which draws sample Lorenz curves and calculates Gini coefficients and Lorenz asymmetry coefficients from data in an Excel sheet Lorenz_for_download_2.zip Diarkibkan 2011-07-26 di Wayback Machine.





















