Gelombang S

Gelombang S, gelombang sekunder, gelombang ricih atau gelombang S anjal ialah sejenis gelombang seismos yang merupakan satu daripada dua jenis gelombang jasad yang anjal, dinamai sedemikian kerana bergerak melalui jasad objek, berbeza dengan gelombang permukaan.
Am[sunting | sunting sumber]
Gelombang S bergerak sebgai gelombang melintang atau ricih, maka gerakannya adalah serenjang dengan arah rambatan gelombang: gelomang S umpama gelombang tali, berbandingh dengan gelombang P yang bergerak melalui slinky. Gelombang ini bergerak melalui bahantara yang anjal, dan daya pemulih yang utamanya datang dari kesan-kesan ricih. Gelombang ini tidak mencapah, sebaliknya mematuhi persamaan keselanjaran untuk bahantara yang tidak boleh dimampatkan:
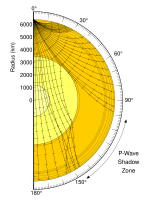
Namanya, S untuk sekunder, datang dari kenyataan bahawa ia merupakan ketibaan langsung yang kedua dalam seismogram gempa bumi, menyusuli gelombang pertama, atau gelombang P, yang berbentuk mampatan, kerana gelombang S berjalan lebih perlahan dalam batu. Tidak seperti gelombang P, gelombang S tidak boleh berjalan melalui teras luar Bumi yang lebur, maka inilah yang menyebabkan zon bayang yang bertentangan dari punca gelombang S. Gelombang S masih boleh melalui teras dalam yang pejal: apabila gelombang P melanda sempadan teras lebur dan pejal, iaitu ketakselanjaran Lehmann, gelombang S pula akan merambat dalam bahantara yang pejal. Kemudian, apabila gelombang S melanda sempadan itu lagi, ia akan menghasilkan gelombang P. Ciri ini membolehkan para ahli seismologi untuk menentukan sifat teras dalam.[1]
Sebagai gelombang melintang, gelombang S menunjukkan sifat-sifat seperti pengutuban dan dwibiasan yang lebih kurang sama seperti gelombang melintang yang lain. Gelombang S yang mengutub pada satah melintang dipanggil gelombang SH, dan yang mengutub pada satah menegak pula dipanggil gelombang SV-. Apabila gelombang S atau P melanda suatu antaramuka pada sudut selain 90 darjah, maka berlakunya fenomena penukaran mod. Seperti yang diterangkan di atas, jika antaramuka itu terletak di antara pepejal dan cecair, S menjadi P dan P juga menjadi S. Bagaimanapun, sungguhpun antaramuka itu adalah antara dua bahantara yang pejal, penukaran mod tetap terjadi. Jika gelombang P melanda antaramuka, mungkin terjadinya empat mod rambatan: P yang dipantulkan dan dipancarkan, dan SV yang dipantulkan dan dipancarakan. Begitu juga, jika gelombang SV melanda antaramuka, empat mod yang sama berlaku dalam perkadaran yang berbeza. Jerayun yang tepat bagi kesemua gelombang ini ditakrifkan oleh persamaan Zoeppritz yang merupakan penyelesaian kepada persamaan gelombang. Gelombang S lebih perlahan daripada gelombang P.
Teori[sunting | sunting sumber]
Ramalam gelombang S mula diteorikan pada tahun 1800-an, mulai dengan hubungan tegasan-terikan untuk pepejal yang isotropi:
yang mana ialah tegasan, dan ialah parameter-parameter Lamé (dengan sebagai modulus ricih), ialah delta Kronecker, dan tensor terikan ditakrifkan seperti berikut:
untuk sesaran terikan u. Apabila rumus tensor terikan dikaitkan pada rumus tegasan-terikan tersebut, maka hasilnya:
Dalam situasi ini, Hukum ke-2 Newton membuahkan persamaan homogen gerakan untuk perambatan gelombang seismos:
yang mana ialah ketumpatan jisim. Apabila dikenakan tensor tegasan tadi, maka hasilnya:
Apabila dikaitkannya kepercaman vektor serta dilakukannya penganggaran yang tertentu, maka persamaan gelombang seismos dalam bahantara homogen ialah:
yang mana tatatanda Newton telah digunakan untuk terbitan masa. Apabila ikal persamaan ini dikaitkan dengan kepercaman vektor, maka hasilnya:
iaitu persamaan gelombang semata-mata yang dikaitkan dengan ikal u dengan halaju untuk memuaskan
Inilah yang menakrifkan perambatan gelombang S. Dengan mengambil kecapahan persamaan gelombang seismos dalam bahantara homogen dan bukan ikal itu, maka hasilnya persamaan yang menakrifkan perembatan gelombang P.
Lihat juga[sunting | sunting sumber]
- Gelombang P
- Gelombang Love
- Gelombang Rayleigh
- Gelombang Lamb
- Gelombang garis bujur
- Gelombang permukaan
- Amaran Awal Gempa Bumi (Jepun)
Rujukan[sunting | sunting sumber]
- ^ University of Illinois at Chicago (17 July 1997). "Lecture 16 Seismographs and the earth's interior". Dicapai pada 8 June 2010.















