Hipotenus

Segi tiga sudut tepat dengan hipotenus.

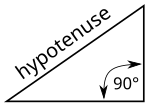
Dalam geometri, hipotenus atau ialah sisi terpanjang pada segi tiga sudut tegak, sisi yang berlawanan dengan sudut tegak. Panjang hipotenus dari segi tiga sudut tegak dapat ditemukan menggunakan teorem Pythagoras yang menyatakan bahwa kuasa dua panjang hipotenus sama dengan jumlah kuasa dua panjang sisi-sisi lainnya. Misalnya, jika salah satu sisi memiliki panjang 3 (dikuasa dua menjadi 9) dan yang lain memiliki panjang 4 (dikuasa dua menjadi 16), maka jumlah ialah 25. Maka, panjang hipotenus ialah punca kuasa dua 25 = 5.

Menghitung hipotenus

al=

Panjang hipotenus dihitung menggunakan fungsi punca kuasa dua yang tersirat oleh teorem Pythagoras. Dengan menggunakan notasi umum bahawa panjang kedua-dua kaki segi tiga (sisi saling tegak lurus) ialah a dan b, dan hipotenus adalah c, maka

$c={\sqrt {a^{2}+b^{2}}}.$

Teorem Pythagoras, dan dengan panjang ini, juga dapat diterbitkan daripada hukum kosinus dengan mengamati bahawa sudut yang berlawanan dengan hipotenus ialah 90° dan mencatat bahawa kosinusnya ialah 0:

$c^{2}=a^{2}+b^{2}-2ab\cos 90^{\circ }=a^{2}+b^{2}\therefore c={\sqrt {a^{2}+b^{2}}}.$

Banyak bahasa komputer mendukung fungsi standar ISO C hypot (x, y), yang mengembalikan nilai di atas. Fungsi ini dirancang agar tidak gagal ketika perhitungan langsung mungkin terlimpah dan menjadi sedikit lebih tepat dan kadang-kadang lebih lambat secara ketara.

Sifat

Dalam gambar, a ialah hipotenus dan b dan c adalah sisi-sisi lain. Projeksi ortografi b ialah m, dan c adalah n.

Unjuran ortografi:

• Panjang hipotenus sama dengan jumlah panjang unjuran ortografi kedua-dua sisi lain.
• Kuasa dua panjang lain sama dengan produk dari panjang unjuran ortografi pada hipotenus darab panjangnya.

b² = a · m

c² = a · n

• Juga, panjang sisi b adalah purata proporsi antara panjang unjuran m dan hipotenus a.

a/b = b/m

a/c = c/n

Nisbah trigonometri

Dengan nisbah trigonometri, seseorang dapat memperoleh nilai dari dua sudut tirus, $\alpha \,$dan $\beta \,$, daripada segi tiga sudut tegak.

Dengan panjang hipotenus $c\,$dan dari sisi $b\,$, nisbah ialah:

${\frac {b}{c}}=\sin(\beta )\,$

Fungsi songsang trigonometri ialah:

$\beta \ =\arcsin \left({\frac {b}{c}}\right)\,$

Dengan $\beta \,$ialah sudut berlawanan dengan sisi $b\,$.

Sudut yang berdekatan sisi $b\,$ ialah $\alpha \,$ = 90° – $\beta \,$

Nilai sudut $\beta \ ,$ juga dapat diperoleh dengan persamaan:

$\beta \ =\arccos \left({\frac {a}{c}}\right)\,$

dengan $a$ adalah sisi lainnya.

Lihat juga

• Trigonometri
• Pythagoras
• Segi tiga