Gelombang sinus

Gelombang sinus atau sinusoid merupakanfungsi matematik yang berbentuk ayunan halus berulang. Fungsi ini sering muncul dalam ilmu matematik, fizik, pemprosesan isyarat, dan teknik elektrik, dan pelbagai jenis bidang lain. Bentuk paling sederhana daripada fungsi ini terhadap waktu )t) adalah:
dimana:
- A, amplitud, adalah puncak simpangan fungsi dari kedudukan tengahnya,
- ω, frekuensi sudut, menunjukkan berapa banyak gerak berulang-alik yang terjadi dalam satu unit waktu, dalam radian per saat,
- φ, fasa, menunjukkan dimana posisi awal gerakan ketika t=0,
- Jika fasa tidak bernilai nol, seluruh gelombang akan nampak bergeser mengikut sumbu X (sumbu waktu) sebesar φ/ω saat. Nilai negatif pada fasa menunjukkan henti, sedangkan nilai positif menunjukkan gelombang "berangkat lebih awal".
Gelombang sinus sangat penting dalam bidang fizik kerana gelombang ini mempertahankan bentuknya ketika ditambahkan kepada gelombang sinus berfrekuensi sama yang lain walaupun fasanya berbeza. Gelombang ini merupakan satu-satunya fungsi berkala yang memiliki sifat ini. Sifat ini menjadikan gelombang ini sebahagian penting dalam Analisis Fourier.
Bentuk Umum[sunting | sunting sumber]
Secara umum, fungsi ini dapat memiliki:
- dimensi ruang, x (kedudukan), dengan frekuensi k (juga disebut nombor gelombang)
- titik tengah amplitud tidak bernilai nol, D (disebut bias DC)
dengan rumus:
Nombor gelombang bergantung pada frekuensi sudut dengan rumus:
dimana λ adalah panjang gelombang, f adalah frekuensi, dan c adalah kecepatan fasa
Persamaan ini menggambarkan gelombang sinus dalam satu dimensi, iaitu persamaan di atas menggambarkan amplitud gelombang pada kedudukan x ketika waktu t dalam satu garis sahaja. Contohnya gelombang pada seutas tali yang digerak-gerakkan[1].
Untuk gelombang yang lebih kompleks, seperti gelombang air yang terbentuk daripada batu yang dilemparkan kedalam kolam, maka diperlukan rumus yang lebih kompleks pula[2].
Contoh kejadian[sunting | sunting sumber]
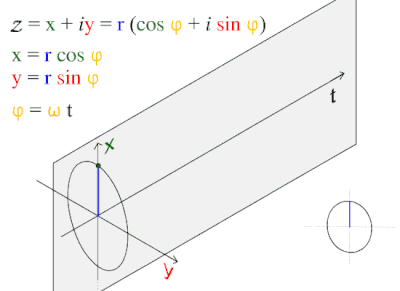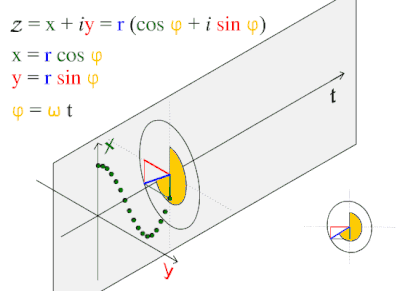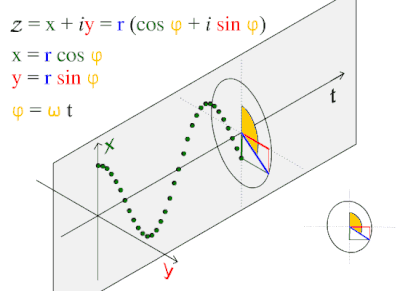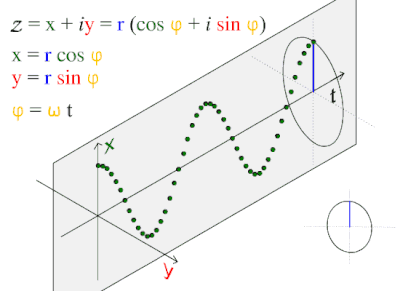
Gelombang ini sering muncul setiap hari, tamsilnya gelombang laut, gelombang suara, dan gelombang cahaya.
Gelombang kosinus merupakan gelombang "sinusoid" kerana sehingga gelombang kosinus sama seperti gelombang sinus dengan pergeseran fasa sebesar n/2. Oleh kerana gelombang ini fasanya lebih maju, sering juga dikatakan fungsi kosinus mendahului gelombang sinus, atau gelombang sinus terlambat dari kosinus[3].
Telinga manusia boleh menangkap gelombang sinus dari udara sebagai suara yang jernih disebabkan hanya memiliki frekuensi tunggal tanpa harmonik; beberapa suara yang mendekati gelombang sinus sempurna adalah siulan, gelas kristal yang dibunyikan dengan menggesekkan hujung jari pada bibir gelas, dan suara yang dihasilkan garfu tala[4].
Gelombang suara yang terdiri daripada beberapa isyarat sinus akan ditangkap telinga sebagai bunyi "berisik" atau memiliki harmonik tertentu; dikatakan suara tersebut memiliki "warna" (timbre).
Siri Fourier[sunting | sunting sumber]

Pada tahun 1822, Joseph Fourier, seorang ahli matematik Perancis, menemui bahawa gelombang sinusoid dapat digunakan untuk membentuk (paling tidak mendekati) semua gelombang berkala, termasuk gelombang persegi. Fourier menggunakan penemuan ini sebagai alat untuk menganalisi gelombang dan aliran panas. Analisis ini sering digunakan dalam pemprosesan isyarat dan analisis statistik siri waktu.
Rujukan[sunting | sunting sumber]
- ^ "salinan arkib". Diarkibkan daripada yang asal pada 2011-07-19. Dicapai pada 2013-03-26.
- ^ http://hyperphysics.phy-astr.gsu.edu/hbase/sound/wavplt.html
- ^ "salinan arkib". Diarkibkan daripada yang asal pada 2011-10-02. Dicapai pada 2013-03-26.
- ^ www.triggertone.com/term/Sine_Wave




