Kerelatifan khas
- Peneranganan pendahuluan tentang rencana ini boleh didapati di Pengenalan kerelatifan khas.
- Bagi sejarah, lihat: Sejarah kerelatifan khas
Kerelatifan khas atau teori kerelatifan khas (Jawi: تيوري كريلاتيفن خاص) merupakan teori fizik yang diterbitkan pada 1905 oleh Albert Einstein dalam rencananya "Mengenai Elektrodinamik Jasad yang Bergerak" (bahasa Inggeris: "On the Electrodynamics of Moving Bodies"). Teori tersebut menggantikan tanggapan Newton tentang ruang dan masa dan melibatkan elektromagnet seperti yang diwakilkan dalam persamaan Maxwell. Teori ini dipanggil "khas" kerana ia melibatkan prinsip kerelatifan hanya pada keadaan tertentu bagi kerangka rujukan inersia dalam ruang masa yang mendatar dan kerangka yang terpecut, iaitu ketika kesan graviti boleh diabaikan.
Kerelatifan khas menghubungkaitkan ruang dan masa ketika laju cahaya (begitu juga pemalar asas yang lain) adalah malar, dan teori membawa kepada satu keadaan ketika dua pemerhati boleh bercanggah tentang selang masa dan jarak di antara dua kejadian, tetapi tanpa bercanggah kejadian yang berlaku. Hal tersebut menunjukkan yang masa boleh berlalu lebih perlahan jika pemerhati bergerak, bergantung kepada laju relatif.
Teori ini turut meramalkan persamaan E=mc².
Postulat[sunting | sunting sumber]
- Postulat pertama - Prinsip kerelatifan – Hukum fizik (termasuk elektrodinamik) semua adalah sama dalam semua rangka rujukan inersia.
- Postulat kedua - Ketakvarianan c - Dalam ruang kosong, cahaya akan merambat dengan halaju malar c, tidak bersandar kepada keadaan pergerakan bagi jasad yang memancarkannya.
Kebanyakan buku teks kini membuat silap termasuk yang laju cahaya tidak bersandar kepada keadaan pergerakan bagi pemerhati yang mengukurnya, seperti sebahagian daripada postulat kedua. Jika dibaca dengan teliti pada kertas Einstein 1905, ia menunjukkan yang Einstein tidak melakukan anggapan begitu. Perdebatan Einstein muncul apabila dia menerbitkan secara mengejut dan menunjukkan keputusan yang tidak dapat dipercayai dari dua anggapan mudah.
Satu daripada anggapan balas tentang itu (dan, seperti yang dinyatakan di atas, melibatkan postulat kedua) ialah laju cahaya dalam vakum, yang diwakilkan dengan c, adalah sama bagi semua pemerhati inersia. Seorang pemerhati yang cuba mengukur laju cahaya akan mendapat jawapan yang sama tidak kira komponen sistem pemerhati bergerak.
Ketiadaan rangka rujukan mutlak[sunting | sunting sumber]
Prinsip kerelatifan, yang menyatakan tiada rangka rujukan pegun, berbalik kepada Galileo, dan digabungkan ke dalam Fizik Newton. Walau bagaimanapun, pada akhir abad ke-19, persamaan Maxwell menyebabkan sesetengah ahli fizik mencadangkan yang alam semesta dipenuhi oleh bahan yang dikenali sebagai "aether" (kadangkala ditulis sebagai "ether") untuk memindahkan gelombang elektromagnet. Aether dikatakan untuk membentuk rangka rujukan mutlak terhadap laju yang boleh diukur. Dalam kata lain, aether adalah satu-satunya benda yang tetap dan pegun dalam alam semesta.
Aether mempunyai sifat yang unik: ia amat kenyal sehingga mampu menanggung gelombang elektromagnet, gelombang yang boleh berinterksi dengan jirim, tetapi ia tidak menyediakan rintangan untuk jasad melaluinya. Juga dipostulatkan bahawa cahaya muncul dari aether yang bergetar. Keputusan dari banyak eksperimen, termasuk eksperimen Michelson-Morley, menunjukkan oleh kerana Bumi sentiasa 'pegun' terhadap Aether — sesuatu yang sukar untuk diterangkan, kerana Bumi berada dalam pusingan mengelilingi matahari. Bagi ramai orang, penyelesaian yang paling sesuai adalah untuk menolak tanggapan Aether dan rangka mutlak, dan mengambil postulat Einstein. Kerelatifan Khas diterbitkan untuk tidak menganggap mana-mana rangka rujukan tertentu sebagai khas; tetapi, dalam kerelatifan, suatu sistem muncul untuk memerhatikan hukum fizik yang sama yang tidak bersandar kepada halaju pemerhati. Terutamanya, halaju cahaya sentiasa diukur sebagai c walaupun diukur oleh pemerhati yang berbeza yang bergerak pada halaju yang berbeza (tetapi malar). Tidak kira betapa lajunya objek itu bergerak, halaju cahaya relatif bagi objek adalah sentiasa c.
Akibat-akibat[sunting | sunting sumber]
Einstein telah menyatakan yang semua kesan-kesan Kerelatifan Khas boleh didapati dari ujian transformasi Lorentz.
Transformasi ini, juga Kerelatifan Khas, membawa kepada ramalan fizik yang berbeza dengan mekanik Newton apabila halaju relatif boleh dibandingkan dengan halaju cahaya. Laju cahaya lebih besar daripada apa yang manusia pernah jumpa hinggakan sesetengah kesan yang diramalkan oleh kerelatifan tidak pernah difikirkan:
- Dilasi masa (Pengembangan masa) - masa yang berlalu di antara dua keadaan adalah tidak berbeza daripada satu pencerap dengan yang lain, tetapi bergantung kepada laju relatif rangka rujukan si pencerap. (cth: paradoks kembar yang memperihalkan seorang kembar yang terbang menghampiri laju cahaya dan apabila kembali, dia mendapati kembarnya telah berusia lebih cepat.)
- Kurang keserentakan - dua perkara yang berlaku serentak bagi satu pencerap mungkin berlaku pada masa yang berlainan bagi pencerap yang lain (kurang keserentakan mutlak ).
- Kontraksi Lorentz (Pengucutan Lorentz) - dimensi (cth: panjang) bagi sesuatu objek seperti yang diukur oleh satu pencerap mungkin lebih kecil dari keputusan pengukuran objek yang sama bagi pencerap yang lain. [[cth: paradoks tangga melibatkan tangga yang panjang bergerak menghampiri laju cahaya dan diisi ke dalam garaj yang lebih kecil.)
- Pertambahan halaju - laju bukanlah ditambah dengan sesuka hati, sebagai contoh, satu roket melepaskan misil pada kelajuan 2/3 halaju cahaya relatif kepada roket tetapi misil itu tidak melepasi halaju cahaya relatif kepada pencerap.
- Jisim dan momentum - apabila memperoleh momentum, jisim ketara objek bertambah seperti tenaga (dan memberi persamaan E=mc2).
Transformasi Lorentz untuk ruang dan masa[sunting | sunting sumber]

Dalam animasi ini, arah menegak menunjukkan masa dan arah mengufuk menunjukkan jarak, garisan putus-putus merupakan trajektori ruang-masa ("garis dunia") bagi pencerap. Suku bawah rajah menunjukkan peristiwa yang boleh dilihat oleh pengguna, dan suku yang atas menunjukkan kon cahaya- yang akan boleh melihat pencerap. Titik kecil adalah peristiwa arbitrari dalam ruang-masa.
Cerun garis dunia (sisihan dari yang menegak) memberikan halaju relatif bagi pencerap. Perhatikan bagaimana pandangan ruang-masa berubah apabila pencerap memecut.
Teori kerelatifan bergantung kepada "rangka rujukan". Suatu rangka rujukan merupakan satu titik di angkasa yang pegun, atau dalam gerakan seragam, dari keadaan yang boleh diukur sepanjang 3 paksi. Sebagai tambahan, rangka rujukan mempunyai jam, yang bergerak bersama rangka rujukan yang membolehkan pengukuran masa untuk apa-apa peristiwa.
Sesuatu peristiwa adalah satu keadaan yang boleh ditetapkan sebagai satu masa dan lokasi unik yang tunggal dalam ruang relatif kepada satu rangka rujukan: Ia adalah satu "titik" dalam ruang-masa. Oleh kerana laju cahaya adalah malar dalam kerelatifan bagi setiap rangka rujukan, denyutan cahaya boleh digunakan untuk mengukur jarak dan merujuk balik masa ketika peristiwa itu berlaku dengan jam, walaupun cahaya mengambil masa untuk tiba ke jam selepas peristiwa itu berlaku.
Contohnya, letupan mercun boleh dikira sebagai satu "peristiwa". Kita boleh tentukan peristiwa dengan lengkap dengan empat koordinat ruang-masa: masa berlaku dan lokasi dalam ruang 3 dimensi dari titik rujukan. Kita anggap rangka rujukan ini sebagai .
Dalam teori kerelatifan, kita lazim mengira posisi sesuatu titik dari rangka rujukan yang lain.
Katakan kita mempunyai rangka rujukan kedua , iaitu paksi ruang dan masa betul-betul sama dengan pada masa adalah sifar, tetapi bergerak pada halaju malar terhadap sepanjang paksi .
Oleh kerana tiada rangka rujukan mutlak dalam teori kerelatifan, konsep 'bergerak' tidak begitu dianggap wujud kerana semuanya sentiasa bergerak. Malah, mana-mana dua rangka yang bergerak dengan laju yang sama pada arah yang sama disebut sebagai segerak (comoving). Maka, dan adalah tidak segerak.
Mari kita jadikan peristiwa tersebut kepada kordinat ruang-masa bagi sistem dan bagi . Maka, transformasi Lorentz mengkhususkan yang koordinat ini berkaitan dengan cara (yang didapati dari putaran ruang masa):
iiatu dipanggil faktor Lorentz dan adalah laju cahaya dalam vakum.
Koordinat dan tidak berubah tetapi paksi dan berubah disebabkan transformasi. Malah, ia membentuk satu putaran.
Kuantiti yang takvarian (tak berubah) dalam transformasi Lorentz dikenali sebagai skalar Lorentz.
Kecutan Lorentz dan dilasi masa[sunting | sunting sumber]
Kita kembangkannya lalu kita akan memperolehi:
Ujian bagi terma persamaan untuk dalam transformasi Lorentz menunjukkan yang semua posisi dalam satu rangka dikalikan dengan gamma, satu nombor yang lebih besar dari satu, untuk mengira selang dalam rangka segerak kedua. Yang ini mungkin akan ditafsirkan dengan betul sebagai kontraksi atau kecutan bagi mana-mana objek dari saiz penuh dan pegun dalam satu rujukan ke rujukan kedua yang sedang bergerak. Terma ini dipanggil Kecutan Lorentz.
Begitu juga bagi persamaan untuk masa , dikalikan dengan gamma dalam rangka kedua. Yang ini mungkin akan ditafsirkan sebagai masa yang secara fiziknya bergerak lebih perlahan apabila suatu objek itu bergerak berbanding yang masa yang berada di dalam rangka objek yang pegun. Terma ini pula dipanggil Dilasi Masa atau Pengembangan Masa.
Mungkin boleh diagak dari satu rangka yang kelihatan kecil, dari rangka rujukan yang dikecutkan, yang lain akan kelihatan kembang; dan begitu juga dengan masa. Walau bagaimanapun, oleh kerana persamaan Lorentz adalah simetri bagi laju relatif yang berlawanan, setiap rangka kelihatan melihat secara paradoks yang lain sama-sama dikecutkan dan masa sama-sama dikembangkan.
Kesan ini bukan sekadar kemunculan; masa yang berada dalam rangka rujukan yang berbeza pada dasarnya juga bergerak pada kadar yang berbeza antara satu sama lain dan panjang objek benar-benar berubah secara fizikal ketika berada dalam gerakan relatif.
Lihat juga paradoks kembar.
Keserentakan[sunting | sunting sumber]
Kerelatifan khas berlaku kepada periatiwa yang serentak dalam satu rangka rujukan dan tidak perlu kepada serentak dalam rangka rujukan yang lain.
Keserentakan boleh dilihat dengan mempertimbangkan terma kedua persamaan Lorentz yang telah dikembangkan bagi . Halaju mengubah dua peristiwa bergerak ke hadapan atau ke belakang dalam masa yang relatif kepada satu sama lain jika kedua-duanya terpisah secara fizikal di angkasa. Ini boleh diperhatikan dalam Rajah 1; sebahagian peristiwa boleh diperhatikan bergerak dari masa silam ke masa depan dan kembali apabila pecutan antara rangka rujukan berlaku dan masa berlalu.
Kurang keserentakan menandakan suatu, sebagai contoh, dua hujung batang yang bergerak tidak sama tuanya - jadi sebagai contoh, batang radioaktif akan lebih tua dan kurang keaktifan di hujung yang belakang dari hujung yang depan. Malah, kurang keserentakan menerangkan mengapa kontraksi Lorentz berlaku — batang disengetkan sepanjang paksi masa ketika memecut membuatkannya kelihatan pendek dalam dimensi ruang.
Menurut kertas kerja oleh saintis Los Alamos, James Terrell, keboleh-cerapan kontraksi Lorentz dari titik tunggal di angkasa adalah mustahil dilakukan oleh peralatan optik. Sebagai contoh, galaksi sfera jauh bergerak merentasi Bima Sakti dengan halaju 0.99c akan muncul sebagai objek sfera dalam peralatan optik kita. Kontraksi Lorentz bagi galaksi jauh tidak dapat dicerap dari Bumi.
Walau bagaimanapun, kontraksi Lorentz adalah kesan fizikal yang benar. Pengukurannya dengan peralatan yang mempunyai ruang besar digunakan secara serentak dalan rangka yang diberikan adalah suatu yang tidak mustahil.
Halangan dan kesan pergerakan melebihi laju cahaya[sunting | sunting sumber]

Dalam rajah 2, selang ibarat 'masa'; dalam kata lain, terdapat rangka rujukan yang peristiwa A dan B berlaku pada lokasi yang sama dalam ruang, dipisahkan oleh masa yang berbeza. Jika A mendahului B dalam rangka itu, maka A mendahului B dalam semua rangka. Ia diandaikan tidak mustahil bagi jirim (atau maklumat) untuk mengembara dari A ke B, maka akan berlaku hubungan sebab dan akibat (dengan A yang menjadi sebab dan B menjadi akibatnya).
Selang AC dalam rajah iabarat 'ruang-masa'; dalam kata lain, terdapat rangka rujukan yang peristiwa A dan C berlaku serentak, dipisahkan oleh ruang. Walau bagaimanapun, terdapat juga rangka yang A mendahului C (seperti yang ditunjukkan) dan rangka yang C mendahului A, maka paradoks logik akan berlaku. Contohnya, jika A penyebabnya, C menjadi akibat, kemudian akan terdapat rangka rujukan yang akibat mendahului sebab. Cara lain untuk melihatnya adalah jika teknologi membolehkan pergerakan yang lebih laju dari cahaya, ia juga akan bertindak sebagai mesin masa. Maka, satu dari akibat kerelatifan khas adalah (dengan menganggap sebab dan akibat dikekalkan sebagai prinsip logik), tiada satupun maklumat mahupun objek berjirim yang boleh bergerak melebihi laju cahaya. Dalam kata lain, situasi logik tidak jelas dalam kes kerelatifan am, maka ia masih dipersoalkan sama ada terdapat prinsip asas yang mengekalkan sebab dan akibat (dan menghalang pergerakan yang lebih laju dari cahaya) dalam kerelatifan am.
Walaupun tanpa mempertimbangkan sebab dan akibat, terdapat sebab yang kukuh mengapa perjalanan yang lebih cepat dari cahaya adalah dilarang oleh kerelatifan khas. Contohnya, jika daya yang malar dikenakan ke atas sesuatu objek bagi masa yang tidak terhad, kemudian mengkamirkan F=dp/dt akan memberikan momentum yang bertambah tanpa batas, tetapi ini disebabkan menghampiri infiniti apabila v</v> menghampiri c. Bagi mana-mana pencerap yang tidak memecut, ia dilihat seperti suatu inersia objek itu bertambah, untuk menghasilkan pecutan yang lebih kecil untuk bertindak ke atas daya yang sama. Keadaan ini dicerap sebagai pemecut zarah.
Penambahan halaju[sunting | sunting sumber]
Jika pemerhati di melihat objek bergerak sepanjang paksi pada halaju , maka pemerhati di sistem akan melihat objek bergerak dengan halaju iaitu:
Persamaan ini boleh diterbitkan dari transformasi ruang-masa di atas. Perhatikan jika objek bergerak pada kelajuan cahaya dalam sistem system (atau ), maka ia akan turut bergerak pada kelajuan cahaya dalam sistem . Juga, jika kedua-dua dan kecil terhadap kelajuan cahaya, kita akan kembali kepada intuitif transformasi halaju Galilean: .
Jisim, momentum, dan tenaga[sunting | sunting sumber]
Sebagai tambahan unutuk mengubah anggapan tentang ruang dan masa, kerelatifan khas memaksa untuk mempertimbangkan konsep jisim, momentum, dan tenaga, iaitu semua yang penting dalam mekanik Newton. Kerelatifan khas menunjukkan yang konsep ini adalah aspek berlainan bagi kuantiti fizik yang sama dalam cara yang sama yang menunjukkan ruang dan masa adalah saling berkaitan.
Terdapat beberapa cara (yang sama) untuk menentukuan momentum dan tenaga dalam kerelatifan khas. Satu cara menggunakan hukum keabadian. Jika hukum ini sah dalam kerelatifan khas, ia mesti benar untuk setiap rangka rujukan yang berkemungkinan. Walau bagaimanapun, jika seseorang melakukan eksperimen fikiran yang mudah dengan menggunakan takrif Newton tentang momentum dan tenaga, dia akan mendapati yang kuantiti ini tidak akan diabadikan dalam kerelatifan khas. Seseorang itu boleh menggunakan idea keabadian dengan membuat sedikit perubahan kepada takrif untuk mengira halaju relatif. Inilah takrif baru yang diambil kira sebagai benar bagi momentum dan tenaga dalam kerelatifan khas.
Diberi satu objek berjirim takvarian m0 yang bergerak dengan halaju v, tenaga dan momentum diberi sebagai
iaitu γ (faktor Lorentz) diberikan
dan c adalah laju cahaya. Terma γ muncul secara kerap dalam kerelatifan, dan datang dari persamaan transformasi Lorentz.
Tenagadan momentum relatif boleh dikaitkan menerusi formula
yang dirujuk sebagai persamaan tenaga-momentum relatif.
Bagi halaju yang lebih kecil dari cahaya, γ yang boleh dianggarkan dengan menggunakan pengembangan siri Taylor dan mendapati yang
Sekiranya tiada terma pertama dalam pernyataan tenaga, formula ini akan menepati takrif biasa bagi momentum dan tenaga kinetik dalam Newtonian. Seperti yang sepatutnya, kerelatifan khas haruslah menepati mekanik Newton pada halaju rendah.
Dengan melihat rumus bagi tenaga di atas, apabila sesuatu objek berada dalam keadaan rehat (v = 0 dan γ = 1) maka terdapat tenaga yang bukan kosong tertinggal:
Tenaga ini dirujuk sebagai tenaga rehat. Tenaga rehat tidak menyebabkan sebarang konflik denga teori Newton kerana ia adalah malar, selagi tenaga kinetik diambil kira, ia berlainan dalam tenaga yang diambil kira.
Dengan mengambil rumus ini pada nilai muka, kita akan melihat dalam kerelatifan, jisim hanyalah satu bentuk tenaga. Pada tahun 1927, Einstein menyatakan tentang kerelatifan khas:
Bawah teori ini, jisim bukanlah magnitud yang tidak terubah, tetapi magnitud yang bergantung kepada (dan, malah, serupa dengan) jumplah tenaga. [1]
Rumus ini menjadi penting apabila mengukur jisim bagi nukleus atom yang berlainan. Dengan melihat perbezaan dalam jisim, seseorang itu boleh meramalkan nukleus yang menyimpan tenaga tambahan yang boleh dileraikan dengan tindak balas nuklear. Maklumat ini menjadi penting dalam pembinaan bom nuklear. Kesan dan pengaruh rumus ini dalam kehidupan abad ke-20 membuatkan persamaan ini sangat terkenal dalam sains.
Jisim kerelatifan[sunting | sunting sumber]
Kursus pengenalan fizik dan sesetengahh buku teks lama tentang kerelatifan khas mentakrifkan jisim relatif yang meningkat apabila halaju sesuatu jasad itu meningkat. Menurut interpretasi geometri kerelatifan khas sering diperbalahkan malah terma 'jisim' septutnya bermaksud 'jisim rehat' lalu tidak bergantung kepada rangka inersia atau takvarian.
Dengan menggunakan makna jisim kerelatifan, jisim sesuatu objek mungkin berubah bergantung kepada rangka inersia pencerap dalam cara yang sama dengan sifat yang lain seperti kepanjangannya. Mentakrifkan kuantiti sebegitu mungkin adakala berguna untuk meringkaskan pengiraan dengan menetapkannya kepada rangka tertentu. Contohnya, katakan suatu jasad dengan jisim takvarian m0 bergerak pada suatu halaju yang relatif kepada sistem rujukan pencerap. Pencerap itu akan mentakrifkan jisim kerelatifan bagi jasad itu adalah:
"Jisim relatif" sepatutnya tidak dikelirukan dengan takrif "jisim membujur" dan "melintang" yang digunakan sekitar 1900 dan diasaskan oleh penggunaan hukum Newton yang tak konsisten: yang menggunakan F=ma bagi jisim pemboleh ubah, manakala jisim relatif bersesuaian dengan jisim dinamik Newton iaitu p=mv dan F=dp/dt.
Perhatikan juga jasad tersebut tidak bertambah dalam rangka yang betul, memandangkan jisim relatif hanya berbeza bagi pencerap yang berada dalam rangka yang berlainan. Satu-satunya jisim yang tidak bergantung kepada rangka adalah jisim takvarian. Apabila menggunakan jisim relatif, rangka rujukan terpakai sepatutnya ditentukan jika ia tidak lagi jelas. Pertambahan jisim relatif tidak bertambah dari penambahan bilangan atom dalam objek. Malah, setiap atom, malah juga setiap zarah subatom meningkatkan jisim relatifnya apabila objek memecut.
Buku-buku teks fizik kadang-kala menggunakan jisim kerelatifan kerana ia membolehkan pelajar menggunakan pengetahuan mereka berkenaan fizik Newton untuk memperoleh tentang kerelatifan dengan rangka pilihan mereka. "Jisim relativistik" juga konsisten dengan konsep "pengembangan masa" dan "pengecutan kepanjangan".
Daya[sunting | sunting sumber]
Takrif klasik bagi daya, F:
juga sah bagi kerelatifan.
Daya adalah masa-terbitan dari momentum, maka rumus klasik bagi hukum Newton kedua perlu digantikan dengan
Seperti yang dilihat dalam persamaan, vektor daya dan pecutan adalah tidak semestinya berselari dalam kerelatifan.
Geometri ruang-masa[sunting | sunting sumber]
Kerelatifan khas menggunakan ruang Minkowski 4-dimensi, yang merupakan contoh ruang-masa. Ruang ini, walau bagaimanapun, amat serupa dengan ruang Euclid 3 dimensi yang biasa, dan mujurlah, mudah digunakan.
Pembezaan bagi jarak (ds) dalam ruang cartesian 3D ditakrifkan sebagai:
iaitu adalah pembezaan bagi ruang 3 dimensi. Dalam geometri kerelatifan khas, dimensi keempat iaitu masa ditambah bersama unit c, maka persamaan pembezaan jarak menjadi:
Dalam banyak situasi, mungkin sesuai untuk menjadikan masa sebagai khayalan, (memudahkan persamaan), iaitu dalam persamaan di atas diogantikan dengan , dan metrik menjadi
Ini, walau bagaimanapun, bukanlah hanya teknik pemudah matematik, tetapi merupakan makna teori yang terpenting kerana ia menunjukkan yang kerelatifan khas adalah simetri putaran bagi ruang-masa kita, sangat serupa dengan simetri putaran bagi raung Euclid. Mendalamkan lagi teori ini bergantung kepada konsep metrik Minkowski seperti yang ditunjukkan di bawah.
Jika kita kurangkan ruang dimensi kepada 2, maka kita boleh mewkilkan fizik dalam ruang 3-D.
Kita perhatikan nol geodesik berada di sepanjang dwikon.
ditakrifkan oleh persamaan
atau
iaitu persamaan bulatan dengan r=c*dt. Jika kita kembangkan ini kepada tiga ruang dimensi, nol geodesik merupakan kon 4 dimensi:
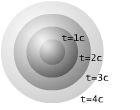
Dwikon nol ini mewakili "garis pandangan" bagi satu titik di angkasa. Iaitu, apabila kita menjenguk bintang dan berkata "Cahaya dari bintang yang aku terima adalah X tahun", kita melihat garis pandangan: nol geodesik. Kita sedang melihat suatu peristiwa meter jauhnya dan d/c saat yang lalu. Bagi sebab ini, dwikon nol juga dikenali sebagai 'kon cahaya'. (Titik di bahagian bawah kiri gambar mewakili bintang, titik asalan mewakili pencerap dan garisan mewakili nol geodesik "garis pandangan".)
Kon di kawasan -t merupakan maklumat yang titik tersebut 'menerima', manakala kon di bahagian +t merupakan maklumat yang titik itu 'menghantar'.
Geometri ruang Minkowski boleh digambarkan dengan menggunakan rajah Minkowski yang juga berguna untuk memahami eksperimen pemikiran dalam kerelatifan khas.
Fizik dalam ruang masa[sunting | sunting sumber]
Setelah mengenali sifat semula jadi ruang masa empat dimensi, kita akan dibawa ke metrik Minkowski, η, diberi dalam komponen (sah dalam mana-mana rangka rujukan) sebagai
Kemudian kita mengenali transformasi koordinat di antara rangka rujukan inersia yang diberi oleh tensor transformasi Lorentz Λ. Bagi kes khas gerakan sepanjang paksi x, kita mempunyai:
iaitu β dan γ ditakrifkan sebagai
Ini memudahkan hampir setiap rumus yang dijumpai dalam kerelatifan khas. Kita faham yang semua kuantiti fizik diberikan oleh tensor. Maka, untuk bertukar dari satu rangka ke rangka yang lain, kita menggunakan hukum tensor transformasi
Untuk lihat betapa bergunanya hukum ini, mula-mula kita mengenali posisi tersebut adalah empat vektor, memandangkan dalam bentuk komponen
Maka, untuk menukarnya dari sistem koordinat S ke sistem S', kita mengira
yang merupakan cara elok untuk sampai ke takrifan transformasi Lorentz yang merumitkan. Tetapi kuasa sebenar menjadi bukti apabila anda mendapati yang semua tensor bertukar dengan peraturan yang sama. Mula-mula, perhatikan yang skalar (sebenarnya kepanjangan posisi empat vektor) terbentuk seperti berikut:
adalah takvarian - dalam kata lain, ia mengambil nilai yang sama dalam semua rangka inersia, hanya kerana ia adalah tensor tahap 0, maka tiada salinan Lorentz muncul dalam transformasinya: |x'| = |x|.
Mengenali yang kuantiti fizik yang lain sebagai tensor juga memudahkan hukum penukaran. Pertama, perhatikan yang halaju empat-vektor U diberi sebagai
Dengan ini, kita boleh menukar hukum tentang penambahan halaju yang kelihatan pelik kepada pernyataan ringkas tentang penukaran halaju empat-vektor bagi satu zarah dari satu rangka ke yang lain. Tenaga-momentum empat-vektor diberi oleh (dan dalam bentuk komponen)
Ini memberikan kita takvarian
Kita boleh dapatkan apakah takvarian ini dengan menyangkal, memandangkan ia adalah satu skalar, tidak kisah rangka rujukan mana yang dikira, dan dengan menukar ke rangka yang momentum keseluruhan adalah sifar. Kemudian kita akan dapat keputusan
Contoh yang selanjutnya bagi tensor fizik adalah tensor medan elektromagnet, dan tensor ketegangan-tenaga, dan sekali lagi transformasinya diberikan oleh hukum transformasi tensor mudah.
Medan elektrik dan medan magnet kini disatukan kepada tensor medan elektromagnet:
Cas ketumpatan dan arus ketumpatan disatukan kepada arus-cas 4-vektor:
dan persamaan Maxwell dikurangkan kepada dua. (lihat Formulasi persamaan Maxwell dalam kerelatifan khas)
(Hukum Ampere-Gauss) (Hukum Faraday-Gauss)
Iaitu merupakan kembangan kecerunan ruang-masa:
Taraf[sunting | sunting sumber]
Kerelatifan khas adalah tepat hanya jika keupayaan graviti adalah kurang dari c^2; dalam medan graviti kerelatifan am perlu digunakan (yang akan menjadi kerelatifan khas pada had medan lemah). Pada skala yang sangat kecil, seperti pada panjang Planck dan di bawah kesan kuantum haruslah diambil kira untuk graviti kuantum. Walau bagaimanapun, pada skala makroskopik dan kehadiran medan graviti yang kuat, kerelatifan khas diuji secara eksperimen mempunyai ketepatan yang sangat tinggi darjahnya (10^-14) dan diterima oleh komuniti ahli fizik. Keputusan eksperiman yang akan bertentangan dengannya takkan terboleh-hasil semula lalu dianggap sebagai ralat eksperimen.
Oleh kerana kebebasan, seseorang harus memilih bagaimana mentakrifkan unit panjang dan masa dalam fizik, ia mungkin untuk membuatkan satu dari dua postulat kerelatifan sebagai kesan tautologi bagi takrifan, tapi seseorang itu tidak boleh lakukannya untuk kedua-dua postulat serentak kerana apabila digabungkan, ia akan memberikan kesan yang tidak bergantung kepada pilihan seseorang tentang takrifan panjang dan masa.
Kerelatifan khas adalah konsisten dan ia adalah bahagian organik bagi teori fizik moden, yang paling ketara adalah teori medan kuantum, teori berangkai dan kerelatifan am (dalam kes tertentu bagi medan graviti yang diabaikan).
Mekanik Newton mengikut secara matematik dari kerelatifan khas pada halaju kecil (berbanding dengan laju cahaya) - maka Mekanik Newton boleh dipertimbangkan sebagai kerelatifan khas bagi jasad yang bergerak lambat. Lihat Status kerelatifan khas bagi perincian yang lebih.
Beberapa eksperimen penting boleh dikatakan membawa kepada kerelatifan khas:
- Eksperimen Trouton-Noble menunjukkan yang tork atas sebuah kapasitor adalah bebas dari segi posisi dan rangka rujukan inersia — eksperimen yang menunjukkan postulat pertama.
- Eksperimen Michelson-Morley yang terkenal yang menunjukkan takvarian berarah bagi laju cahaya dua hala - "laju cahaya" seperti yang ditakrifkan dalam postulat kedua.
Beberapa eksperimen telah dijalankan untuk menguji kerelatifan khas untuk menentang teori saingan. Ini termasuklah:
- Eksperimen Kaufman — pesongan elektron menurut ramalan Lorentz-Einstein
- Eksperimen Hamar — tiada "halangan aliran ether"
- Eksperimen Kennedy-Thorndike — pengembangan masa menurut transformasi Lorentz
- Eksperimen Rossi-Hall — kesan kerelatifan ke atas separuh hayat zarah yang bergerak pantas
- Eksperimen untuk menguji teori pemancar menguji yang laju cahaya adalah tidak bersandar kepada laju pemancar.
Sebagai tambahan, pemecut zarah berfungsi hampir setiap hari dan sering memecut dan mengukur sifat zarah yang bergerak hampir ke kelajuan cahaya. Banyak kesan dapat dilihat dalam pemecut zarah yang sama dengan teori kerelatifan dan tidak seiring dengan mekanik Newton.
Lihat juga[sunting | sunting sumber]
- Orang: Albert Einstein | Alexander MacFarlane | Arthur Eddington | Bernhard Riemann | Harry Bateman | Hendrik Lorentz | Henri Poincare | Hermann Minkowski | Robert S. Shankland
- Kerelatifan: Anti-kerelatifan | Kerelatifan am | Prinsip kerelatifan | Rangka rujukan | Rangka rujukan inersia | Teori kerelatifan | Transformasi Lorentz
- Fizik: Hipotesis seretan eter | Kesan Doppler | Keserentakan | Kosmologi | Laju cahaya | Mekanik Newtonian | Persamaan kerelatifan Euler | Ruang-masa
- Matematik: Empat-vektor | Garis dunia | Geometri | Kon cahaya | Kumpulan Lorentz | Kumpulan Poincare | Nombor pisahan-kompleks Ruang Minkowski | Tensor
- Falsafah: Aktualisme | Formalisme | Konvensionalisme
Pautan luar[sunting | sunting sumber]
- (Inggeris)The Hogg Notes tentang Kerelatifan Khas Pengenalan kepada kerelatifan khas bagi tahap ijazah].
- (Inggeris)Kalkulator kerelatifan Pengiraan geometri bagi masalah kerelatifan seperti penambahan halaju. Perhatikan yan ia adalah asas-Java dan mengambil beberapa minit sekiranya menggunakan modem 56k.
- (Inggeris)Kerelatifan dalam konteks Sejarah Penemuan kerelatifan khas.
- (Inggeris)Tentang kerelatifan Terdapat bayak cara untuk menerbitkan transformasi Lorentz dengan kemalaran Einstein tentang postulat cahaya.
- (Inggeris)Pantulan Kerelatifan Buku dalam talian lengkap tentang kerelatifan dengan bibliografi tambahan.
- (Inggeris)Nota Kuliah Kerelatifan Khas merupakan pengenalan kepada kerelatifan khas dan mengandungi penerangan berilustrasi dari Universiti Negeri dan Institut Politeknik Virginia.
- (Inggeris)Brane World Mach Principles dan Eksperimen Michelson-Morley Diarkibkan 2006-09-28 di Wayback Machine
- (Inggeris)Teori kerelatifan khas Pendekatan baru untuk menerangkan makna teoretikal bagi Kerelatifan Khas dari panangan geometri.
- (Inggeris)Kerelatifan Khas Univesiti Stanford, Helen Quinn, 2003
- (Inggeris)Menerusi Mata Einstein Universiti Kebangsaan Australia (Australian National University). Kesan visual kerelatifan diteragka bersama gambar bergerak dan imej.
- (Inggeris)Greg Egan's Foundations.
- (Inggeris)Cahaya Einstein Sebuah anugerah penerangan pegenalan tanpa teknikal (klip filem dan demonstrasi) disokong oleh penerangan dan animasi pada tahap dengan matematik atau tanpanya.
- (Inggeris)Enlightening Ideas Diarkibkan 2011-04-24 di Wayback Machine animasi humor tentang kerelatifan khas bagi masyarakat umum, Yannick Mahé, 2005
- (Inggeris)Warp Special Relativity Simulator program komputer yang menunjukkan kesan bergerak menghampiri kelajuan cahaya.
- (Inggeris)Tutorial Kerelatifan Caltech Diarkibkan 2006-10-02 di Wayback Machine Pengealan asas kepada konsep Keelatifan Khas dan Am, memerlukan pengetahuan asas tentang geometri.
- (Inggeris)"Einstein Benar (Lagi):Eksperimen Mengesahkan E= mc2" Pengukuran terkini bagi persamaan Einstein tepat kepada "persepuluh ribu bagi satu bahagian dalam sejuta."
Rujukan[sunting | sunting sumber]
Buku teks[sunting | sunting sumber]
- (Inggeris) Einstein, Albert. "Relativity: The Special and the General Theory".
- (Inggeris) Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (edisi ke-4). Syarikat W. H. Freeman. ISBN 0-7167-4345-0
- (Inggeris) Schutz, Bernard F. A First Course in General Relativity, Percetakan Universiti Cambridge. ISBN 0-521-27703-5
- (Inggeris) Taylor, Edwin, dan Wheeler, John (1992). Spacetime physics (edisi ke-2). Syarikat W.H. Freeman. ISBN 0-7167-2327-1
- (Inggeris) Einstein, Albert (1996). The Meaning of Relativity. Fine Communications. ISBN 1-56731-136-9
- (Inggeris) Geroch, Robert (1981). General Relativity From A to B. Percetakan Universiti Chicago. ISBN 0-226-28864-1
Rencana jurnal[sunting | sunting sumber]
- (Inggeris) On the Electrodynamics of Moving Bodies, A. Einstein, Annalen der Physik, 17:891, 30 Jun 1905 (dalam bahasa Inggeris)
- (Inggeris) Wolf, Peter and Gerard, Petit. "Satellite test of Special Relativity using the Global Positioning System", Physics Review A 56 (6), 4405-4409 (1997).
- (Inggeris) Will, Clifford M. "Clock synchronization and isotropy of the one-way speed of light", Physics Review D 45, 403-411 (1992).
- (Inggeris) Alvager et al., "Test of the Second Postulate of Special Relativity in the GeV region", Physics Letters 12, 260 (1964).
Subbidang am dalam Fizik
| |
|
Biofizik | Fizik atom, molekul, dan optik | Fizik jirim termeluwap | Fizik zarah | Keelektromagnetan | Kerelatifan am | Kerelatifan khas | Mekanik klasik | Mekanik kontinum | Mekanik kuantum | Mekanik statistik | Teori medan kuantum | Termodinamik | |



















































![{\displaystyle T_{\left[j_{1}',j_{2}',...j_{q}'\right]}^{\left[i_{1}',i_{2}',...i_{p}'\right]}=\Lambda ^{i_{1}'}{}_{i_{1}}\Lambda ^{i_{2}'}{}_{i_{2}}...\Lambda ^{i_{p}'}{}_{i_{p}}\Lambda _{j_{1}'}{}^{j_{1}}\Lambda _{j_{2}'}{}^{j_{2}}...\Lambda _{j_{q}'}{}^{j_{q}}T_{\left[j_{1},j_{2},...j_{q}\right]}^{\left[i_{1},i_{2},...i_{p}\right]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69d0d85be920d9a0780a4eeece6e22f1d8ef7087)







![{\displaystyle [E_{x},E_{y},E_{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9610285cc67bea4b5ef29d7f7ead4b6175539bd9)
![{\displaystyle [B_{x},B_{y},B_{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5001f5bd38c7abb8616cc14cf2adfc9d1b5c89e)


![{\displaystyle [J_{x},J_{y},J_{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50d98e28ca9a1cb76738b1a6417b95bfc8f78abc)





