Pecahan
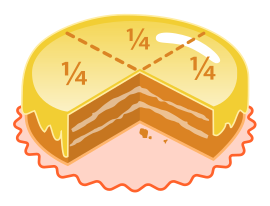
Pecahan (Bahasa Inggeris: fraction daripada Bahasa Latin fractus, "dipecahkan") ialah nombor yang mewakili sebahagian daripada keseluruhan atau sekumpulan benda.
Pecahan terawal ialah salingan integer-integer yang menggunakan simbol mewakili satu perdua, satu pertiga, satu perempat, dan seterusnya.[1]
Dalam perkembangan seterusnya, pecahan "kasar" atau pecahan biasa telah dibangunkan dan ia masih digunakan sehingga hari ini. Pecahan ini terdiri daripada satu pengangka dan satu penyebut, pengangka mewakili beberapa bahagian sama dan penyebut menunjukkan berapa banyak bahagian-bahagian tersebut yang membentuk keseluruhan. Sebagai contoh dalam pecahan 3/4, pengangka, 3, menunjukkan 3 bahagian sama, sementara penyebut, 4, menunjukkan yang 4 bahagian yang membentuk keseluruhan.
Kemudian, pecahan perpuluhan pula diperkenalkan, yang kini hanya dikenali sebagai "perpuluhan". Penyebutnya ialah nombor asas sepuluh yang dikuasakan dengan nombor yang ditentukan oleh bilangan digit di kanan titik perpuluhan. Jadi, nombor perpuluhan 0.75 mempunyai pengangka 75 dan penyebut 10 kuasa 2 (kerana terdapat 2 digit di kanan titik perpuluhan). Jadi penyebutnya ialah 100.
Jenis pecahan ketiga yang sering digunakan ialah "peratusan", yang menggunakan penyebut 100 sahaja. Jadi, 75 peratus bermaksud 75/100.
Dalam matematik, set untuk semua pecahan (kasar) dipanggil set nombor nisbah dan diwakili simbol Q.
Penggunaan lain pecahan adalah untuk menunjukkan nisbah dan pembahagian. Jadi, pecahan 3/4 juga digunakan untuk menunjukkan nisbah 3:4 (tiga kepada empat) dan pembahagian 3 ÷ 4 (tiga dibahagikan dengan empat).
Istilah[sunting | sunting sumber]
Mengikut sejarah, "pecahan" merujuk kepada sebarang nombor yang tidak mewakili keseluruhan, nombor yang kini dipanggil "perpuluhan", asalnya dikenali sebagai "pecahan perpuluhan"; dan nombor yang kini dipanggil "pecahan", asalnya dikenali sebagai "pecahan kasar", perkataan "kasar" (vulgar) bermaksud "biasa" (commonplace).
Perkataan pecahan juga digunakan dalam ungkapan matematik seperti pecahan lanjar dan pecahan algebra.
Menulis pecahan[sunting | sunting sumber]
Pecahan biasa atau kasar biasanya ditulis dalam satu pasangan nombor, nombor di atas dikenali sebagai pengangka sementara yang di bawah dikenali sebagai penyebut. Lazimnya, satu garisan memisahkan keduanya. Jika garisan ini mencondong, ia digelar solidus atau slash, contoh 3⁄4. Jika garisannya melintang, ia digelar vinculum atau secara tidak rasmi, "palang pecahan", seperti: .
Tanda solidus boleh diabaikan dari gaya mencondong (cth. 34), yang mengurangkan ruang tetapi masih memberi makna dalam konteksnya, ia banyak digunakan dalam isyarat lalu lintas di beberapa negara.
Dalam paparan komputer dan tipografi, beberapa pecahan dinyatakan dalam satu angka. Antaranya:
- ¼ (satu perempat)
- ½ (satu perdua)
- ¾ (tiga perempat)
- ⅓ (satu pertiga)
- ⅔ (dua pertiga)
- ⅛ (satu perlapan)
- ⅜ (tiga perlapan)
- ⅝ (lima perlapan)
- ⅞ (tujuh perlapan)
Penggunaan[sunting | sunting sumber]
Pecahan lebih banyak digunakan apabila penyebutnya kecil. Adalah mudah untuk mendarab 32 dengan 3⁄16, berbanding mendarabnya dengan nombor perpuluhan untuk pecahan tersebut, (0.1875). Adalah juga lebih tepat mendarab 15 dengan 1⁄3, berbanding mendarabnya dengan nombor perpuluhan untuk satu pertiga (0.333...). Untuk mengubah satu pecahan menjadi nombor perpuluhan, bahagikan pengangka dengan penyebut, dan bundarkan kepada ketepatan yang diingini.
Bentuk pecahan[sunting | sunting sumber]
Pecahan biasa, pecahan wajar dan pecahan tak wajar[sunting | sunting sumber]
Pecahan kasar (atau pecahan biasa) ialah satu nombor nisbah yang ditulis dengan satu integer (pengangka) yang dibahagikan dengan satu integer bukan sifar (penyebut).
Satu pecahan kasar akan menjadi pecahan wajar apabila nilai mutlak pengangka adalah kurang dari nilai mutlak penyebut; yang menjadikan nilai mutlak keseluruhan pecahan kurang daripada 1. Pecahan kasar akan menjadi pecahan tak wajar apabila nilai mutlak pengangka adalah lebih besar atau sama dengan nilai mutlak penyebut (cth. 9⁄7).[2]
Nombor bercampur[sunting | sunting sumber]
Nombor bercampur ialah campuran nombor bulat dan pecahan wajar. Penambahan ini dinyatakan tanpa menggunakan tanda operasi seperti "+"; sebagai contoh, untuk merujuk 2 kek penuh dan 1 kek dengan tiga perempat bahagian, bahagian penuh dan bahagian pecahan itu ditulis bersebelahan. .
Satu pecahan tak wajar boleh digunakan untuk menyatakan satu nombor bercampur, seperti . Boleh dibayangkan yang setiap kek penuh itu dibahagikan kepada empat bahagian, menjadikan penyebut untuk kek penuh (nombor bulat) sama dengan penyebut kek yang telah dipotong, . Jadi, setiap kek penuh diwakili dengan pecahan , jadi ialah cara lain untuk menulis nombor bercampur .
Nombor bercampur boleh ditukar menjadi pecahan tak wajar dalam tiga langkah:
- Darabkan nombor bulat dengan penyebut pecahan.
- Tambah pengangka pecahan pada hasil darab di atas.
- Hasil tambah langkah 2 adalah pengangka untuk pecahan (tak wajar) baru, dengan penyebut 'baru' nya kekal sama dengan penyebut untuk pecahan asal nombor bercampur.
Sebaliknya, pecahan tak wajar juga boleh ditukar menjadi nombor bercampur:
- Bahagikan pengangka dengan penyebut.
- Hasil bahagi (tanpa baki) menjadi nombor bulat manakala bakinya menjadi pengangka untuk pecahan.
- Penyebut baru untuk pecahannya adalah sama dengan pecahan tak wajar yang asal.
Pecahan setara[sunting | sunting sumber]
Dengan mendarab pengangka dan penyebut sesuatu pecahan dengan nombor yang sama (bukan sifar), hasil pecahan yang baru adalah setara dengan pecahan asal. Perkataan setara di sini bermaksud, kedua-dua pecahan memiliki nilai yang sama yang mengekalkan integriti yang sama - Perimbangan dan perkadaran yang sama. Ini adalah benar kerana mana-mana nombor , didarab dengan adalah sama dengan pendaraban dengan satu, dan sebarang nombor yang didarab dengan satu mempunyai nilai yang sama dengan nombor asal. Contohnya, untuk pecahan : apabila kedua-dua pengangka dan penyebut didarab dengan 2, hasilnya adalah , yang memiliki nilai yang sama (0.5) dengan . Untuk gambaran lebih jelas, bayangkan kek (dalam gambar di atas) dipotong menjadi empat bahagian; 2 dari empat bahagian ini () mewakili separuh kek ().
Contoh: , , dan kesemuanya adalah pecahan setara.
Membahagikan pengangka dan penyebut dengan nombor (bukan sifar) yang sama juga menghasilkan pecahan setara. Ia dikenali sebagai mengurangkan atau memudahkan pecahan. Satu pecahan yang pengangka dan penyebutnya tidak mempunyai faktor yang sama (selain 1) adalah dianggap tidak boleh dimudahkan dan berada dalam bentuk termudah atau sebutan terendah. Sebagai contoh, bukanlah satu pecahan termudah kerana 3 dan 9 mempunyai faktor yang sama iaitu 3. Sebaliknya, ialah pecahan termudah kerana satu-satunya faktor untuk 3 dan 8 ialah 1.
Salingan dan "penyebut halimunan"[sunting | sunting sumber]
Salingan sesuatu pecahan ialah pecahan dengan pengangka dan penyebutnya diterbalikkan. Contohnya, salingan untuk , ialah .
Oleh kerana hasil bahagi sebarang nombor dengan 1 adalah sama dengan nombor itu, nombor bulat juga boleh ditulis dalam pecahan dengan menggunakan 1 sebagai penyebut: 17 = (kadang-kadang 1 dirujuk sebagai "penyebut halimunan"). Maka, kecuali untuk sifar, setiap pecahan atau nombor bulat memiliki satu salingan. Salingan untuk 17 ialah .
Pecahan kompleks[sunting | sunting sumber]
Pecahan kompleks (atau pecahan majmuk) ialah pecahan yang pengangka atau penyebutnya mengandungi pecahan. Contohnya, dan merupakan pecahan kompleks. Untuk memudahkan satu pecahan kompleks, bahagikan pengangka dengan penyebut seperti dalam pecahan yang lain (lihat bahagian pembahagian untuk keterangan lebih lanjut):
Aritmetik dengan pecahan[sunting | sunting sumber]
Seperti juga nombor bulat, pecahan mematuhi hukum ketertukartertiban, kesekutuan, dan ketaburan, dan hukum melarang pembahagian dengan sifar.
Membandingkan pecahan[sunting | sunting sumber]
Untuk membandingkan pecahan-pecahan yang memiliki penyebut yang sama, cuma memerlukan pembandingan pada pengangkanya.
- kerana 3>2.
Satu cara untuk membanding pecahan yang mempunyai penyebut yang berbeza ialah dengan mencari penyebut yang sama. Untuk membanding dan , ia ditukar menjadi dan . Kemudian, bd adalah penyebut yang sama dan kedua-dua pengangka ad dan bc boleh dibandingkan.
- ? memberikan
Terdapat satu jalan mudah yang dikenali sebagai "pendaraban silang", yang boleh membandingkan ad dan bc, tanpa mengira penyebutnya.
- ?
Darabkan 17 dengan 5 (85) dan darabkan 18 dengan 4 (72). Oleh kerana 85 adalah lebih besar daripada 72, .
Kaedah lain untuk membandingkan pecahan ialah dengan melihat pada pengangkanya. Jika kedua-dua pecahan memiliki pengangka yang sama, maka pecahan yang memiliki penyebut yang lebih kecil adalah pecahan yang lebih besar. Ini kerana, apabila penyebut adalah lebih besar, pengangka akan dibahagikan menjadi bahagian-bahagian yang lebih kecil.
Perlu juga diingat yang setiap nombor negatif, termasuk pecahan negatif, adalah kurang daripada sifar, dan setiap nombor positif, termasuk pecahan positif, adalah lebih daripada sifar, jadi setiap pecahan negatif adalah kurang daripada pecahan positif.[3]
Penambahan[sunting | sunting sumber]
Hukum pertama penambahan pecahan ialah cuma kuantiti serupa yang boleh ditambah; contohnya, penambahan antara kuantiti perempat. Untuk penambahan kuantiti tak serupa, seperti menambah pertiga dengan perempat, keduanya perlu ditukar menjadi kuantiti serupa terlebih dahulu. Bayangkan sebuah saku mengandungi dua perempat, dan saku yang lain mengandungi tiga perempat; jumlahnya adalah lima perempat. Oleh kerana empat perempat adalah bersamaan dengan satu, ia boleh dinyatakan seperti berikut:
- .

Menambah kuantiti tak serupa[sunting | sunting sumber]
Untuk menambah pecahan yang mengandungi kuantiti tak serupa (seperti perempat dan pertiga), adalah perlu untuk menukar kesemuanya menjadi kuantiti serupa. Ia boleh dilakukan dengan mendarab penyebut setiap pecahan.
Bagi menambah perempat dengan pertiga, keduanya ditukar kepada (perduabelas).
Lihat contoh penambahan dua kuantiti di bawah:
Pertama, tukar menjadi perduabelas dengan mendarab pengangka dan penyebut dengan tiga: . adalah bersamaan dengan 1, jadi adalah sama dengan .
Kedua, tukar menjadi perduabelas dengan mendarab pengangka dan penyebut dengan empat: . adalah bersamaan dengan 1, jadi adalah sama dengan .
Kesimpulannya:
Adalah bersamaan dengan:
Kadang-kadang terdapat penyebut yang lebih kecil boleh digunakan (penyebut sepunya terkecil). Contohnya, untuk menambah dan , penyebut 48 boleh digunakan (hasil darab 4 dan 12), tetapi penyebut 12 yang lebih kecil boleh juga digunakan, yang merupakan faktor sepunya terkecil untuk 4 dan 12.
Kaedah ini boleh dinyatakan dalam rumus algebra:
Dan untuk ungkapan yang mengandungi penambahan tiga pecahan:
Penolakan[sunting | sunting sumber]
Secara dasarnya, proses penolakan pecahan adalah sama dengan penambahan; mencari penyebut sepunya, dan tukar setiap pecahan kepada pecahan setara dengan penyebut yang dipilih. Hasil tolak kedua-dua pecahan akan mempunyai penyebut tersebut, dan hasil tolak pengangka untuk pecahan asal. Contohnya,
Pendaraban dan pembahagian[sunting | sunting sumber]
Mendarab dengan nombor bulat[sunting | sunting sumber]
Perhatikan contoh kek seperti di atas, jika satu perempat kek tersebut didarab dengan tiga, hasilnya ialah tiga perempat. Ia boleh digambarkan dalam pengiraan seperti berikut:
Contoh lain, katakan terdapat lima orang bekerja untuk tiga jam bagi setiap tujuh jam waktu bekerja (tiga pertujuh jam waktu bekerja). Secara keseluruhan, mereka bekerja 15 jam (5 x 3 jam seorang), atau 15 pertujuh sehari. Oleh kerana 7 pertujuh bersamaan dengan 1 hari bekerja dan 14 pertujuh bersamaan dengan 2 hari bekerja, jumlah waktu bekerja untuk kelima-lima perkerja adalah 2 hari dan satu pertujuh jam dalam sehari. Dalam pengiraan:
Mendarab dengan pecahan[sunting | sunting sumber]
Perhatikan contoh kek seperti di atas, jika satu perempat kek didarab dengan satu pertiga kek, hasilnya ialah satu perduabelas kek. Dalam erti kata lain, satu pertiga dari satu perempat (atau satu pertiga darab satu perempat) ialah satu perduabelas. Kenapa? kerana setiap bahagian satu perempat telah dipotong menjadi 3 bahagian, dan empat bahagian kek didarab dengan tiga akan menjadi 12 bahagian (atau perduabelas). Ini boleh dinyatakan dalam pengiraan seperti berikut:
Untuk contoh lain, katakan terdapat lima orang yang melakukan kerja yang sama dalam jumlah masa tiga jam daripada tujuh jam waktu bekerja. Setiap orang akan melakukan satu perlima dari 3 jam tersebut, menjadikan jam bekerja mereka satu perlima dari tiga pertujuh dalam sehari. Dalam pengiraan:
Secara umumnya, apabila pecahan didarab, kedua-dua pengangka akan didarab untuk menghasilkan pengangka yang baru, dan kedua-dua penyebut akan didarab untuk menghasilkan penyebut yang baru. Contohnya:
Apabila mendarab (atau membahagi), kaedah pemansuhan silang untuk nombor yang mempunyai faktor sepunya, boleh dilakukan. Contohnya:
2⁄7 X 7⁄8 = 2 1⁄7 1 X 7 1⁄8 4 = 1⁄1 X 1⁄4 = 1⁄4
Nombor dua adalah faktor sepunya untuk pengangka pecahan kiri dan penyebut pecahan kanan, jadi kedua-duanya dibahagikan dengan dua. Manakala nombor tujuh adalah faktor sepunya untuk penyebut pecahan kiri dan pengangka pecahan kanan, dan kedua-duanya dibahagikan dengan tujuh.
Nombor bercampur[sunting | sunting sumber]
Apabila mendarab nombor bercampur, adalah lebih mudah jika nombor bercampur itu ditukar menjadi pecahan tak wajar. Contohnya:
Dalam erti kata lain, adalah sama dengan , menghasilkan jumlah 11 perempat (kerana 2 kek, setiap satu dipotong kepada empat bahagian, menjadikan jumlah keseluruhan 8 perempat (bahagian).) dan 33 perempat adalah sama dengan (kerana 8 kek, setiap satunya dipotong empat, menjadikan jumlah keseluruhan 32 perempat (bahagian).).
Pembahagian[sunting | sunting sumber]
Untuk membahagi dengan satu pecahan yang lain, cuma darabkan dengan salingan pecahan tersebut (diterbalikkan).
Untuk memahami bagaimana ia dilakukan, lihat keterangan berikut:
- 6 inci dibahagikan dengan 3 inci = 2 ,bermaksud kita boleh bahagikan 6 inci kepada 2 bahagian yang berukuran 3 inci setiap satu.
- 6 batu dibahagikan dengan 3 batu = 2, bermaksud kita boleh bahagikan 6 batu kepada 2 bahagian yang berukuran 3 batu setiap satu.
- 6/2 dibahagikan dengan 3/2 = 2, bermaksud kita boleh bahagikan 6/2 kepada 2 bahagian yang bersaiz 3/2 setiap satu.
Untuk pembahagian pecahan-pecahan yang mempunyai penyebut yang sama, cuma bahagikan pengangkanya sahaja dan buangkan penyebutnya. Tapi bagaiman jika pecahan-pecahan itu memiliki penyebut yang berbeza?
Penyelesaiannya ialah, cari penyebut sepunya dan bahagikan pengangkanya, seperti dalam rumus berikut:
- Bagaimanpun, kaedah ini adalah terlalu panjang. Sebaliknya, kaedah "balik dan darab" yang memberikan jawapan yang sama, adalah lebih ringkas.
Ini adalah satu bukti matematik untuk pembahagian menggunakan kaedah balik dan darab.
- Teorem
-
- Bukti
-
- Diketahui yang pembahagian didefinasikan sebagai kebalikan pendaraban. Iaitu,
- jika dan hanya jika
- Dalam ungkapan yang kita mahu buktikan, darabkan pembahagi dengan hasil bahagi yang kemudian dimudahkan menjadi .
- Jadi,
Cara lain untuk memahaminya adalah seperti berikut:
- Soalan, adakah
- Diberi/Diterima
- I. Sebarang nombor yang dibahagikan dengan dirinya adalah bersamaan dengan satu (contoh: )
- II. Apabila satu nombor didarabkan dengan satu, ia tidak berubah (contoh: )
- III. Jika dua pecahan memiliki penyebut sepunya, pengangkanya boleh dibahagikan untuk mendapatkan hasil bahagi (contoh: )
- Bukti
- 1. , Masalah
- 2. , darabkan pecahan pertama dengan dan pecahan kedua dengan , yang sama dengan pendaraban dengan satu, dan seperti yang diterima di atas (I & II) tidak mengubah nilai pecahan tersebut.
-
- Nota: Nilai satu dipilih untuk mendapatkan penyebut sepunya untuk pecahan tersebut; bd adalah penyebut sepunya.
-
- 3. , dari apa yang diberi dalam (III)
- 4. , tatatanda berubah
- 5. , boleh dilihat
- 6. , penyelesaian
Sekitar 4,000 tahun dahulu, orang Mesir purba membahagi pecahan menggunakan kaedah yang sedikit berbeza. Mereka menggunakan gandaan sepunya terkecil dengan pecahan unit. Kaedah ini memberikan jawapan yang sama seperti kaedah moden kita.[4]
Menukar nombor perpuluhan berulang menjadi pecahan[sunting | sunting sumber]
Walaupun nombor perpuluhan lebih berguna apabila melakukan pengiraan, ia tidak memiliki ketepatan seperti yang ada pada pecahan biasa. Kadang-kadang, nombor perpuluhan tak terhingga digunakan untuk mendapatkan ketepatan yang sama. Jadi, adalah lebih berguna jika nombor perpuluhan berulang ditukar menjadi pecahan.
Untuk corak pengulangan yang coraknya bermula selepas titik perpuluhan, pembahagian ringkas corak tersebut dengan nombor sembilan (bergantung pada jumlah nombor dalam corak tersebut), dapat menyelesaikan masalah ini. Contohnya (corak pengulangan ditebalkan):
- 0.555555555555… = 5/9
- 0.626262626262… = 62/99
- 0.264264264264… = 264/999
- 0.629162916291… = 6291/9999
Jika nombor sifar mendahului corak pengulangan selepas titik perpuluhan, nombor sembilan akan diakhiri dengan bilangan sifar yang sama:
- 0.0555… = 5/90
- 0.000392392392… = 392/999000
- 0.00121212… = 12/9900
Dalam kes terdapat nombor perpuluhan yang tidak berulang mendahului corak pengulangan (seperti 0.1523987987987…), asingkan nombor tidak berulang dan nombor berulang dalam penambahan seperti berikut:
- 0.1523 + 0.0000987987987…
Kemudian, tukar kedua-duanya menjadi pecahan. Oleh kerana bahagian pertama tidak mempunyai corak berulang, ia tidak boleh ditukar mengikut corak yang diberi di atas:
- 1523/10000 + 987/9990000
Tambahkan kedua-dua pecahan dengan mencari penyebut sepunya...
- 1521477/9990000 + 987/9990000
Tambahkan keduanya menjadi
- 1522464/9990000
Akhir sekali, mudahkan hasilnya:
- 31718/208125
Rasionalisasi[sunting | sunting sumber]
Rasionalisasi pecahan adalah satu teknik memudahkan penyebut untuk ungkapan pecahan yang rumit, seperti . Ia sangat berguna dalam pengiraan yang melibatkan nombor kompleks seperti . Satu pecahan perlu dirasionalkan jika penyebutnya mengandungi nombor tak nisbah, nombor khayalan atau nombor kompleks agar pengiraan menjadi lebih mudah. Proses rasionalisasi adalah melibatkan pendaraban bahagian atas dan bawah pecahan dengan konjugat penyebut untuk menjadikan penyebutnya satu nombor nisbah. Walaupun proses ini menyebabkan pengangka boleh bertukar menjadi tak nisbah atau kompleks, proses ini masih boleh memudahkan manipulasi dengan mengurangkan bilangan nombor tak nisbah dalam penyebut, atau dengan membuat penyebutnya menjadi nyata, dalam kes ungkapan yang kompleks.
Kes istimewa[sunting | sunting sumber]
- Pecahan unit ialah pecahan biasa dengan pengangka 1, contoh. .
- Pecahan Mesir ialah hasil tambah pelbagai pecahan unit yang berbeza, contoh.. Istilah ini adalah bersempena dengan fakta yang orang Mesir purba mengungkapkan semua pecahan kecuali , dan dalam bentuk ini.
- Pecahan diadik ialah pecahan biasa yang memiliki penyebut dalam gandaan nombor dua (yang dikuasakan). Contoh. .
Satu ungkapan yang memiliki bentuk pecahan tetapi sebenarnya mewakili pembahagian dengan nombor tak nisbah sering disebut "pecahan tak nisbah". Contoh biasa ialah , sukatan radian untuk sudut kanan.
Nombor nisbah ialah medan hasil bahagi untul integer. Fungsi nisbah adalah fungsi yang dinilai dalam bentuk pecahan, yang pengangka dan penyebutnya adalah polinomial. Ungkapan nisbah ini adalah medan hasil bahagi untuk polinomial (melampaui beberapa domain integer).
- Pecahan lanjar ialah satu ungkapan seperti
- yang ai adalah integer. Ini bukan satu elemen dalam medan hasil bahagi.
- Istilah pecahan separa digunakan dalam algebra untuk mengurai ungkapan nisbah (satu pecahan dengan ungkapan algebra dalam penyebutnya). Tujuannya ialah untuk menulis ungkapan nisbah sebagai jumlah ungkapan nisbah yang lain dengan penyebut yang darjahnya lebih rendah. Sebagai contoh, ungkapan nisbah boleh ditulis semula sebagai hasil tambah untuk dua pecahan: dan . Ini berguna untuk pengiraan beberapa kamiran dalam kalkulus.
Lihat juga[sunting | sunting sumber]
Rujukan[sunting | sunting sumber]
- ^ Howard Eves, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0, "Orang Mesir purba telah berusaha untuk mengelakkan kesukaran pengiraan menggunakan pecahan dengan menyatakan semua pecahan, kecuali 2/3, sebagai satu hasil tambah pecahan unit..Jadi, 2/7 telah dinyatakan sebagai 1/4 + 1/28." Buku ini mengandungi gambarajah simbol-simbol yang digunakan oleh orang Mesir untuk pecahan. "Satu perempat" kelihatan seperti satu bentuk segi empat yang dihitamkan dengan satu garisan bujur di atasnya, 2/3 adalah seperti satu bentuk bujur dengan U terbalik merentasinya.
- ^ World Wide Words: Vulgar fractions
- ^ Visual Fractions tutorial
- ^ Milo Gardner (December 19, 2005). "Math History". Dicapai pada 2006-01-18. Check date values in:
|date=(bantuan) See for examples and an explanation.























































































