Paralaks bintang

Paralaks bintang ialah peralihan ketara bagi kedudukan (paralaks) mana-mana bintang berdekatan (atau objek lain) terhadap latar belakang bintang jauh. Secara lanjutnya, ia kaedah untuk menentukan jarak ke bintang melalui trigonometri, kaedah paralaks bintang. Dicipta oleh kedudukan orbit Bumi yang berbeza, anjakan yang diperhatikan yang sangat kecil adalah terbesar pada selang masa kira-kira enam bulan, iaitu apabila Bumi berada di sisi bertentangan Matahari dalam orbitnya, memberikan jarak garis dasar kira-kira dua unit astronomi antara cerapan. Paralaks itu sendiri dianggap separuh daripada maksimum ini, kira-kira setara dengan anjakan pemerhatian yang akan berlaku disebabkan oleh kedudukan Bumi dan Matahari yang berbeza, iaitu garis dasar satu unit astronomi (AU).
Paralaks bintang sangat sukar untuk dikesan sehinggakan kewujudannya menjadi subjek perdebatan dalam astronomi selama ratusan tahun. Thomas Henderson, Friedrich Georg Wilhelm von Struve, dan Friedrich Bessel membuat pengukuran paralaks pertama yang berjaya pada tahun 1832–1838, untuk bintang Alpha Centauri, Vega dan 61 Cygni.
Kaedah paralaks[sunting | sunting sumber]
Prinsip[sunting | sunting sumber]
Sepanjang tahun kedudukan bintang S diperhatikan berbanding dengan kedudukan bintang lain dalam kejiranan ketara:
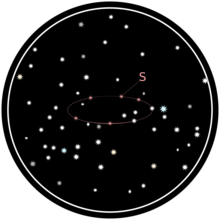
Bintang yang kelihatan tidak bergerak dalam hubungan antara satu sama lain digunakan sebagai titik rujukan untuk menentukan laluan S.
Laluan yang diperhatikan ialah elips: unjuran orbit Bumi mengelilingi Matahari melalui S ke latar belakang bintang yang tidak bergerak yang jauh. Semakin jauh S dialihkan dari paksi orbit Bumi, semakin besar kesipian laluan S. Pusat elips sepadan dengan titik di mana S akan dilihat dari Matahari:
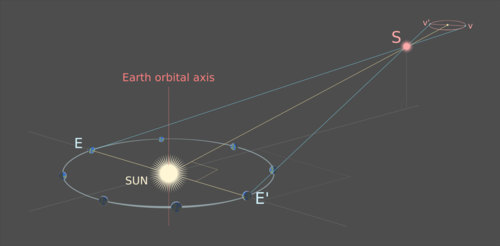
Satah orbit Bumi berada pada satu sudut kepada garis dari Matahari melalui S. Bucu v dan v' unjuran elips laluan S ialah unjuran kedudukan Bumi E dan E' supaya garis E-E' bersilang. garis Sun-S pada sudut tepat; segi tiga yang dicipta oleh titik E, E' dan S ialah segi tiga sama kaki dengan garis Matahari-S sebagai paksi simetrinya.
Mana-mana bintang yang tidak bergerak di antara cerapan adalah, untuk tujuan ketepatan ukuran, sangat jauh. Ini bermakna jarak pergerakan Bumi berbanding jarak ke bintang-bintang yang jauh tak terhingga ini adalah, dalam ketepatan ukuran, 0. Oleh itu, garis penglihatan dari kedudukan pertama Bumi E ke bucu v pada asasnya adalah sama dengan garis penglihatan dari kedudukan kedua Bumi E' ke bucu v yang sama, dan oleh itu akan berjalan selari dengannya - mustahil untuk digambarkan dengan meyakinkan dalam imej saiz terhad:

Memandangkan garis E'-v' ialah rentas dalam satah yang sama (kira-kira secara Euclidean) sebagai garis selari Ev dan E'-v, maka sudut persilangan yang sepadan bagi garis selari ini dengan rentas rentas ini adalah kongruen: sudut θ antara garis penglihatan Ev dan E'-v' adalah sama dengan sudut θ antara E'-v dan E'-v', iaitu sudut θ antara kedudukan diperhatikan S dalam hubungan dengan persekitaran bintang yang kelihatan tidak bergerak.
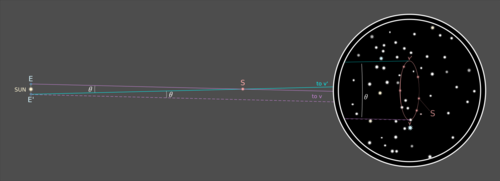
Jarak d dari Matahari ke S kini mengikuti kaedah trigonometri mudah:
tan(½θ) = E-Matahari / d,
supaya d = E-Matahari / tan(½θ), dengan E-Matahari ialah 1 AU.
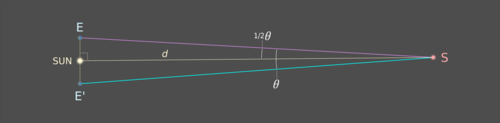
Semakin jauh sesuatu objek, semakin kecil paralaksnya.
Ukuran paralaks bintang diberikan dalam unit kecil arkasaat, atau bahkan dalam seperseribu arkasaat (miliarkasaat). Unit jarak parsek ditakrifkan sebagai panjang kaki segi tiga tepat bersebelahan dengan sudut satu lengkok pada satu bucu, iaitu kaki yang satu lagi ialah sepanjang 1 AU. Memandangkan paralaks dan jarak bintang semuanya melibatkan segi tiga tepat tirus seperti itu, penghampiran trigonometri yang mudah boleh digunakan untuk menukar paralaks (dalam arkasaat) kepada jarak (dalam parsek). Jarak anggaran hanyalah salingan paralaks: Contohnya, Proxima Centauri (bintang terdekat dengan Bumi selain Matahari), yang paralaksnya ialah 0.7685, ialah 1 / 0.7685 parsek = 1.301 parsec (4.24 ly) jauh.
Varian[sunting | sunting sumber]
Paralaks bintang paling kerap diukur menggunakan paralaks tahunan, ditakrifkan sebagai perbezaan kedudukan bintang seperti yang dilihat dari Bumi dan Matahari, iaitu sudut yang dicakup pada bintang dengan jejari min orbit Bumi mengelilingi Matahari. Parsek (3.26 tahun cahaya) ditakrifkan sebagai jarak paralaks tahunan iaitu 1 arkasaat. Paralaks tahunan biasanya diukur dengan memerhatikan kedudukan bintang pada masa yang berbeza dalam setahun semasa Bumi bergerak melalui orbitnya.
Sudut yang terlibat dalam pengiraan ini adalah sangat kecil dan dengan itu sukar untuk diukur. Bintang terdekat dengan Matahari (dan juga bintang dengan paralaks terbesar), Proxima Centauri, mempunyai paralaks 0.7685 ± 0.0002 arkasaat. Sudut ini adalah lebih kurang yang dicakup oleh objek berdiameter 2 sentimeter yang terletak 5.3 kilometer jauhnya.
Terbitan[sunting | sunting sumber]
Untuk segi tiga tepat,
iaitu ialah paralaks, 1 au (149,600,000 km) ialah kira-kira jarak purata dari Matahari ke Bumi, dan ialah jarak ke bintang. Menggunakan anggaran sudut kecil (sah apabila sudut kecil berbanding 1 radian),
jadi paralaks, diukur dalam arkasaat, ialah
Jika paralaks ialah 1", maka jaraknya ialah
Ini mentakrifkan parsek, unit mudah untuk mengukur jarak menggunakan paralaks. Oleh itu, jarak, diukur dalam parsek, adalah mudah , apabila paralaks diberikan dalam arkasaat.[1]
Ralat[sunting | sunting sumber]
Pengukuran jarak paralaks yang tepat mempunyai ralat yang berkaitan. Ralat dalam sudut paralaks yang diukur ini tidak diterjemahkan terus kepada ralat untuk jarak, kecuali ralat yang agak kecil. Sebabnya ialah ralat ke arah sudut yang lebih kecil mengakibatkan ralat jarak yang lebih besar berbanding ralat ke arah sudut yang lebih besar.
Walau bagaimanapun, anggaran ralat jarak boleh dikira dengan
iaitu d ialah jarak dan p ialah paralaks. Anggaran jauh lebih tepat untuk ralat paralaks yang relatif kecil kepada paralaks daripada ralat yang agak besar. Untuk hasil yang bermakna dalam astronomi bintang, ahli astronomi Belanda Floor van Leeuwen mengesyorkan bahawa ralat paralaks tidak melebihi 10% daripada jumlah paralaks semasa mengira anggaran ralat ini.[2]
Sejarah pengukuran[sunting | sunting sumber]
Teori dan percubaan awal[sunting | sunting sumber]

Paralaks bintang adalah sangat kecil sehingga ia tidak dapat diperhatikan sehingga abad ke-19, dan ketiadaannya yang jelas digunakan sebagai hujah saintifik untuk menentang heliosentrisme semasa zaman moden awal. Jelas daripada geometri Euclid bahawa kesannya tidak dapat diperhati jika bintang-bintang berada cukup jauh, tetapi atas pelbagai sebab, jarak jauh yang terlibat kelihatan sama sekali tidak masuk akal: ia adalah salah satu bantahan utama Tycho Brahe terhadap heliosentrisme Copernicus yang selama ini ia serasi dengan kekurangan paralaks bintang yang boleh diperhatikan, perlu ada kekosongan yang besar dan tidak mungkin antara orbit Zuhal dan sfera kelapan (bintang tetap).[3]
James Bradley mula-mula cuba mengukur paralaks bintang pada tahun 1729. Pergerakan bintang terbukti terlalu tidak kecil untuk teleskopnya, tetapi dia sebaliknya menemui aberasi cahaya[4] dan penutatan paksi Bumi, dan mengkatalogkan 3,222 buah bintang.
Abad ke-19 dan ke-20[sunting | sunting sumber]


Pengukuran paralaks tahunan ialah cara pertama yang boleh dipercayai untuk menentukan jarak ke bintang terdekat. Pada suku kedua abad ke-19, kemajuan teknologi mencapai tahap yang memberikan ketepatan dan ketepatan yang mencukupi untuk pengukuran paralaks bintang. Pengukuran paralaks bintang pertama yang berjaya dilakukan oleh Thomas Henderson di Cape Town Afrika Selatan pada 1832–1833, di mana dia mengukur paralaks salah satu bintang terdekat, Alpha Centauri.[5][6] Antara 1835 dan 1836, ahli astronomi Friedrich Georg Wilhelm von Struve di balai cerap universiti Dorpat mengukur jarak Vega, menerbitkan keputusannya pada tahun 1837.[7] Friedrich Bessel, rakan Struve, menjalankan kempen pemerhatian yang sengit pada 1837–1838 di Balai Cerap Koenigsberg untuk bintang 61 Cygni menggunakan heliometer, dan menerbitkan keputusannya pada tahun 1838.[8][9] Henderson pula menerbitkan keputusannya pada tahun 1839, selepas kembali dari Afrika Selatan.
Ketiga-tiga keputusan itu, dua daripadanya diukur dengan instrumen terbaik pada masa itu (pembias besar Fraunhofer yang digunakan oleh Struve dan heliometer Fraunhofer oleh Bessel) adalah yang pertama dalam sejarah untuk mewujudkan skala jarak yang boleh dipercayai ke bintang.[10]
Heliometer besar dipasang di Balai Cerap Kuffner (Di Vienna) pada tahun 1896, dan digunakan untuk mengukur jarak ke bintang lain dengan paralaks trigonometri.[11] Menjelang 1910, ia telah mengira 16 jarak paralaks ke bintang lain, daripada hanya 108 jumlah yang diketahui sains pada masa itu.[11]

Memandangkan sangat sukar untuk diukur, hanya kira-kira 60 data paralaks bintang yang telah diperolehi menjelang akhir abad ke-19, kebanyakannya menggunakan mikrometer filar. Astrograf menggunakan plat fotografi astronomi mempercepatkan proses pada awal abad ke-20. Mesin pengukur plat automatik[12] dan teknologi komputer yang lebih canggih pada tahun 1960-an membenarkan penyusunan katalog bintang yang lebih cekap. Pada tahun 1980-an, peranti terganding cas (CCD) menggantikan plat fotografi dan mengurangkan ketidakpastian optik kepada satu miliarkasaat.
Paralaks bintang kekal sebagai piawai untuk menentukur kaedah pengukuran lain (lihat tangga jarak kosmik). Pengiraan jarak yang tepat berdasarkan paralaks bintang memerlukan pengukuran jarak dari Bumi ke Matahari, kini diketahui dengan ketepatan yang sangat baik berdasarkan pantulan radar dari permukaan planet.[13]
Astrometri ruang[sunting | sunting sumber]

Pada tahun 1989, satelit Hipparcos telah dilancarkan terutamanya untuk mendapatkan paralaks dan gerakan wajar bagi bintang-bintang berdekatan, meningkatkan bilangan data paralaks bintang yang diukur kepada ketepatan miliarkasaat seribu kali ganda. Walaupun begitu, Hipparcos hanya mampu mengukur sudut paralaks untuk bintang sehingga kira-kira 1,600 tahun cahaya jauhnya, lebih sedikit daripada satu peratus diameter Galaksi Bima Sakti.
Teleskop Hubble WFC3 kini mempunyai ketepatan 20 hingga 40 mikroarkasaat, membolehkan pengukuran jarak yang boleh dipercayai sehingga 3,066 parsec (10,000 ly) untuk sebilangan kecil bintang.[15] Ini memberikan lebih ketepatan kepada tangga jarak kosmik dan meningkatkan pengetahuan tentang jarak di Alam Semesta, berdasarkan dimensi orbit Bumi.
Apabila jarak antara dua titik cerapan bertambah, kesan visual paralaks juga menjadi lebih jelas. Kapal angkasa New Horizons NASA melakukan pengukuran paralaks antara bintang pertama pada 22 April 2020, mengambil imej Proxima Centauri dan Wolf 359 berkebetulan dengan balai cerap berasaskan bumi. Kedekatan relatif kedua-dua bintang digabungkan dengan jarak 6.5 bilion kilometer (kira-kira 43 AU) kapal angkasa dari Bumi menghasilkan paralaks arkaminit yang boleh dilihat, membolehkan paralaks dilihat secara visual tanpa instrumentasi.[16]

Misi Gaia oleh Agensi Angkasa Eropah, yang dilancarkan pada 19 Disember 2013, dijangka mengukur sudut paralaks kepada ketepatan 10 mikroarkasaat untuk semua bintang sederhana terang, sekali gus memetakan bintang berdekatan (dan berpotensi planet) sehingga jarak puluhan ribu tahun cahaya dari Bumi.[18] Keluaran Data 2 pada tahun 2018 mendakwa bahawa ralat min untuk paralaks magnitud ke-15 dan bintang yang lebih cerah 20–40 mikroarkasaat.
Astrometri radio[sunting | sunting sumber]
Interferometri garis dasar yang sangat panjang dalam jalur radio boleh menghasilkan imej dengan resolusi sudut kira-kira 1 miliarkasaat, dan oleh itu, untuk sumber radio yang terang, ketepatan ukuran paralaks yang dibuat dalam radio boleh melebihi teleskop optik seperti Gaia. Pengukuran ini cenderung kepada kepekaan terhad, dan perlu dibuat satu demi satu, jadi kerja biasanya dilakukan hanya untuk sumber seperti pulsar dan binari sinar-X, yang pancaran radio adalah kuat berbanding dengan pancaran optik.
Lihat juga[sunting | sunting sumber]
- Tempat ketara
- TAU (kapal angkasa) (projek misi angkasa lepas yang akan menggunakan paralaks)
Rujukan[sunting | sunting sumber]
- ^ Similar derivations are in most astronomy textbooks. See, e.g., Zeilik & Gregory 1998, § 11-1.
- ^ van Leeuwen, Floor (2007). Hipparcos, the new reduction of the raw data. Astrophysics and space science library. 350. Springer. m/s. 86. ISBN 978-1-4020-6341-1. Diarkibkan daripada yang asal pada 2015-03-18.
- ^ See p.51 in The reception of Copernicus' heliocentric theory: proceedings of a symposium organized by the Nicolas Copernicus Committee of the International Union of the History and Philosophy of Science, Torun, Poland, 1973, ed. Jerzy Dobrzycki, International Union of the History and Philosophy of Science. Nicolas Copernicus Committee; ISBN 90-277-0311-6, ISBN 978-90-277-0311-8
- ^ Buchheim, Robert (4 October 2007). The Sky is Your Laboratory. ISBN 978-0-387-73995-3. Page 184.
- ^ Henderson, Thomas (1839). "On the Parallax of α Centauri". Monthly Notices of the Royal Astronomical Society. 4 (19): 168–170. Bibcode:1839MNRAS...4..168H. doi:10.1093/mnras/4.19.168.
- ^ Henderson, Thomas (1840). "On the Parallax of α Centauri". Memoirs of Royal Astronomical Society. 11: 61–68. Bibcode:1840MmRAS..11...61H.
- ^ von Struve, Friedrich Georg Wilhelm (1837). "Stellarum duplicium et multiplicium mensurae micrometricae per magnum Fraunhoferi tubum annis a 1824 ad 1837 in specula Dorpatensi institutae". Astronomische Nachrichten. 14 (16): 249–252. Bibcode:1837AN.....14..249S. doi:10.1002/asna.18370141609.
- ^ Zeilik & Gregory 1998.
- ^ Bessel, FW, "Bestimmung der Entfernung des 61sten Sterns des Schwans Diarkibkan 2007-06-24 di Wayback Machine" (1838) Astronomische Nachrichten, vol. 16, pp. 65–96.
- ^ Reid, Mark (2020). "The first stellar parallaxes revisited". Astronomische Nachrichten. 341 (9): 860–869. arXiv:2009.11913. Bibcode:2020AN....341..860R. doi:10.1002/asna.202013833.
- ^ a b Habison, Peter (1998). "Astrometry and early astrophysics at Kuffner Observatory in the late 19th century". Acta Historica Astronomiae. 3: 93–94. Bibcode:1998AcHA....3...93H. ISSN 0003-2670.
- ^ CERN paper on plate measuring machine USNO StarScan
- ^ Zeilik & Gregory 1998, § 22-3.
- ^ "Hubble stretches the stellar tape measure ten times further". ESA/Hubble Images. Dicapai pada 12 April 2014.
- ^ Harrington, J.D.; Villard, Ray (10 April 2014). "NASA's Hubble Extends Stellar Tape Measure 10 Times Farther into Space". NASA. Dicapai pada 17 October 2014. Riess, Adam G.; Casertano, Stefano; Anderson, Jay; Mackenty, John; Filippenko, Alexei V. (2014). "Parallax Beyond a Kiloparsec from Spatially Scanning the Wide Field Camera 3 on the Hubble Space Telescope". The Astrophysical Journal. 785 (2): 161. arXiv:1401.0484. Bibcode:2014ApJ...785..161R. doi:10.1088/0004-637X/785/2/161.
- ^ Talbert, Tricia (2020-06-10). "New Horizons Conducts the First Interstellar Parallax Experiment". NASA. Diarkibkan daripada yang asal pada 2023-11-04. Dicapai pada 2021-05-20.
- ^ Talbert, Tricia (2020-07-10). "New Horizons Conducts the First Interstellar Parallax Experiment". NASA (dalam bahasa Inggeris). Diarkibkan daripada yang asal pada 2023-11-04. Dicapai pada 2020-07-14.
- ^ Henney, Paul J. "ESA's Gaia Mission to study stars". Astronomy Today. Dicapai pada 8 March 2008.
Bacaan lanjut[sunting | sunting sumber]
- Dyson, F. W. (1915). "Measurement of the distances of the stars". The Observatory. 38: 292. Bibcode:1915Obs....38..292D.









